※所用軟體為Cabri 3D※下載網址

※Using software is Cabri 3D. ※Download website

1.安裝完後，便可觀看和瀏覽以下檔案。

2.開啟Cabri 3D後，如想知曉製圖過程。點擊F11可開啟製圖流程觀看。※註：請先開啟 F8，點選顯示隱藏物件。

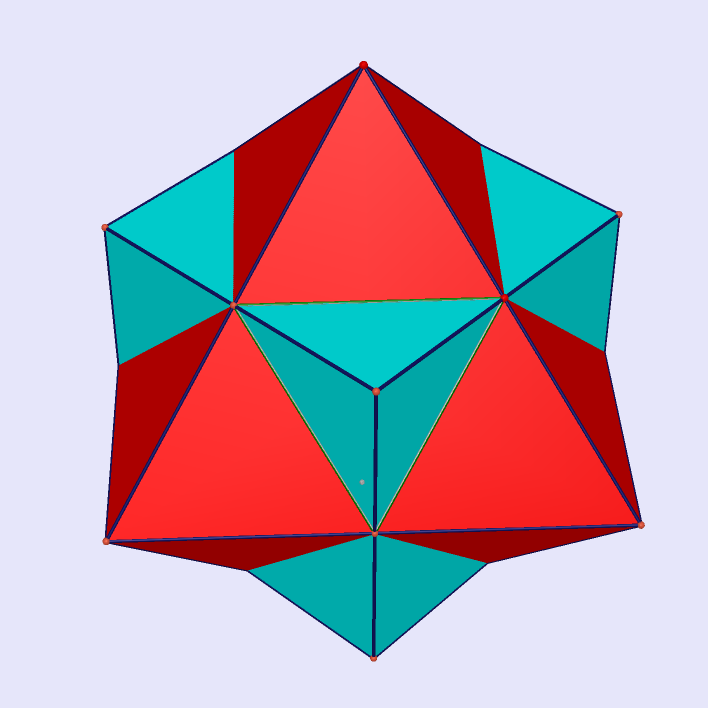
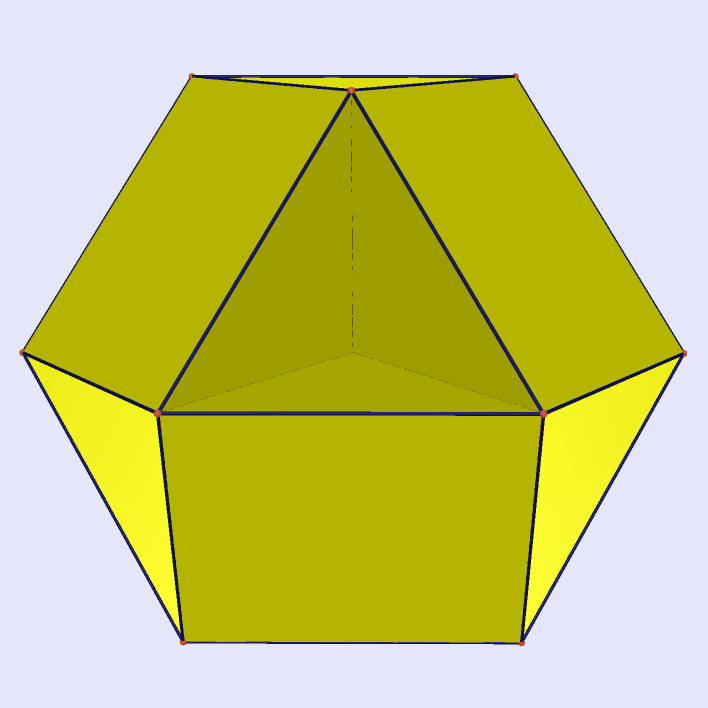
Cube and Its Dual		Cuboctahedron by Square		Cuboctahedron by Triangle
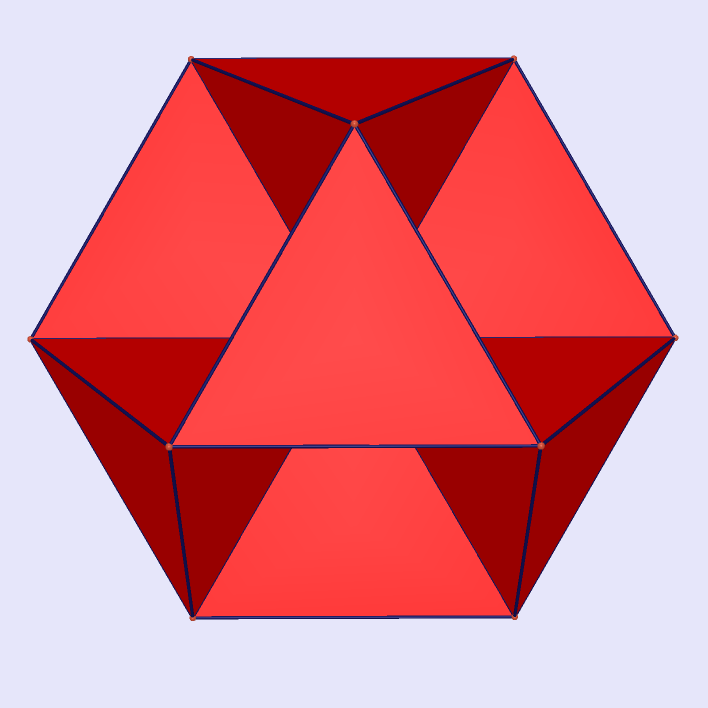
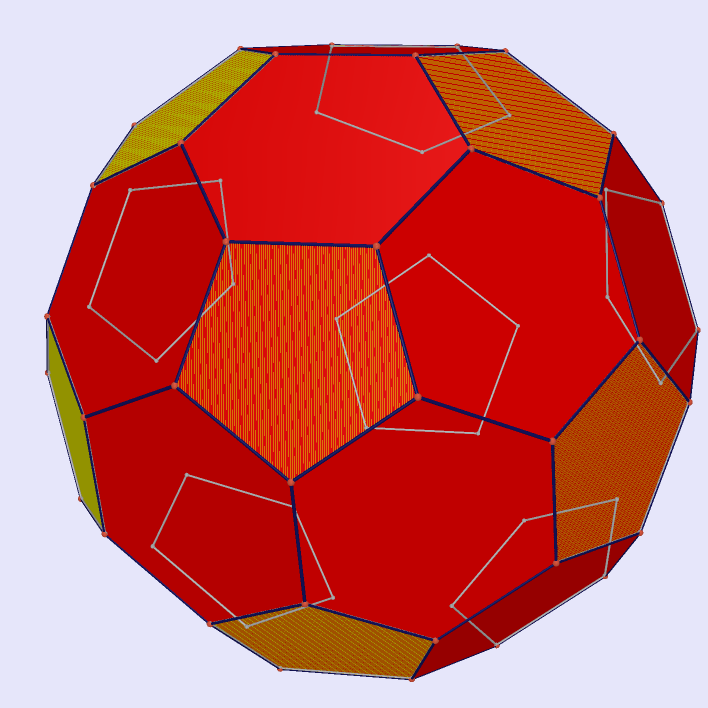
Cuboctahedron		Dodecahedron and Its Dual		Fullerene
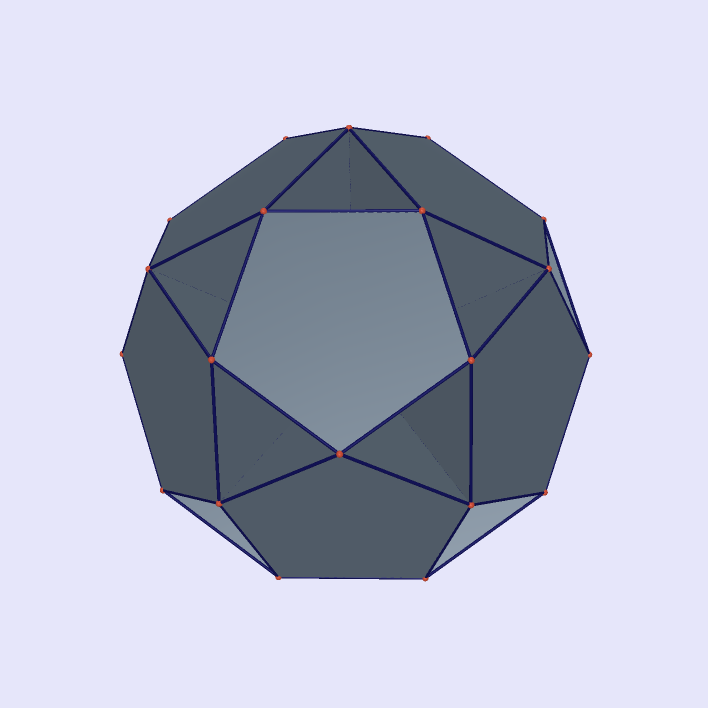
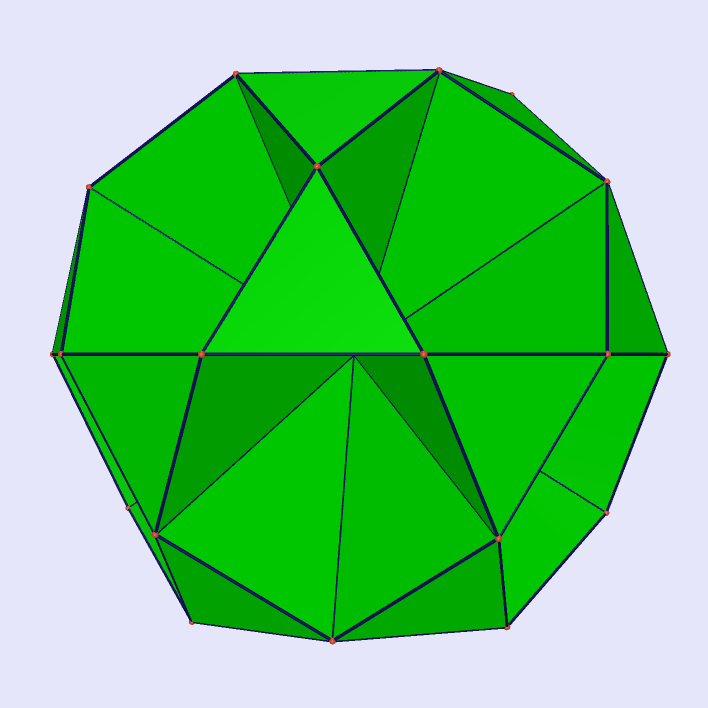
Icosidodecahedron by Pentagon		Icosidodecahedron by Triangle		Icosidodecahedron
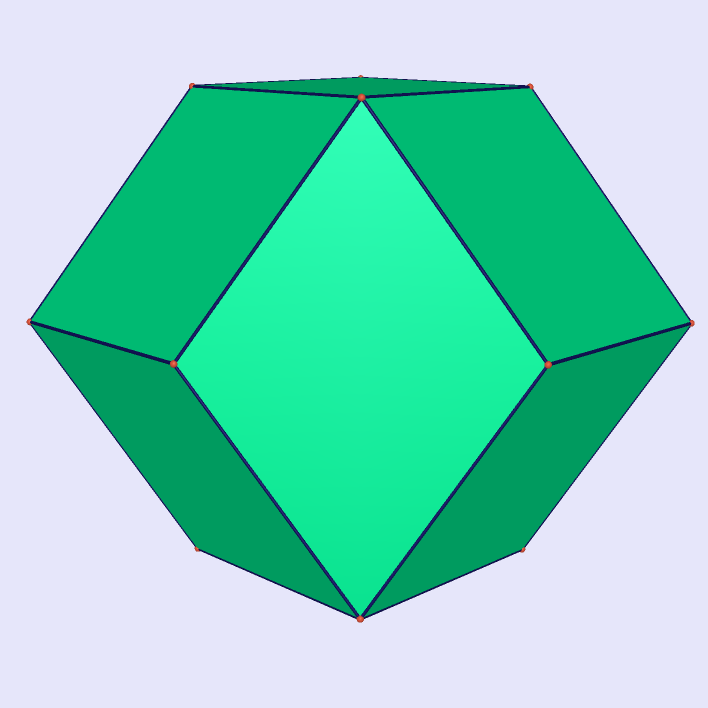
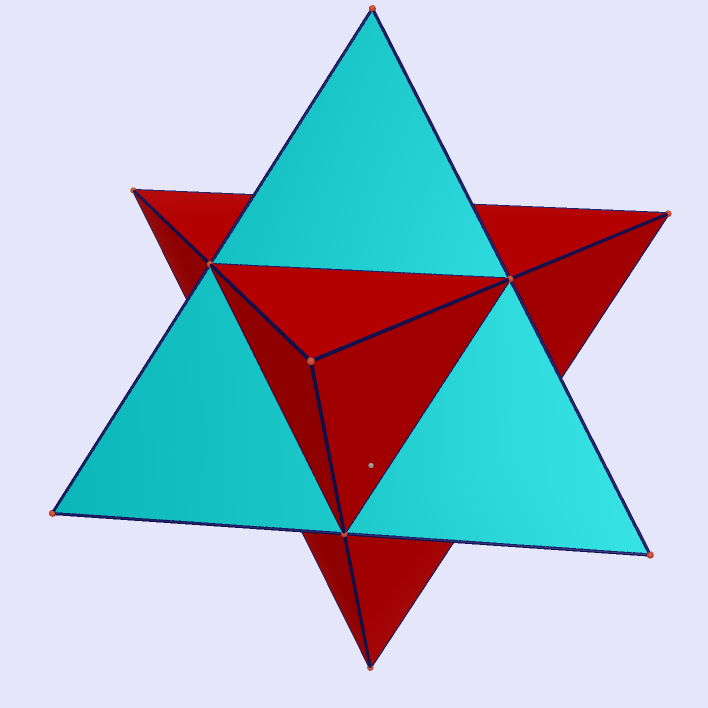
Rhombic Dodecahedron		Rhombic Triacontahedron		Stella Octangula
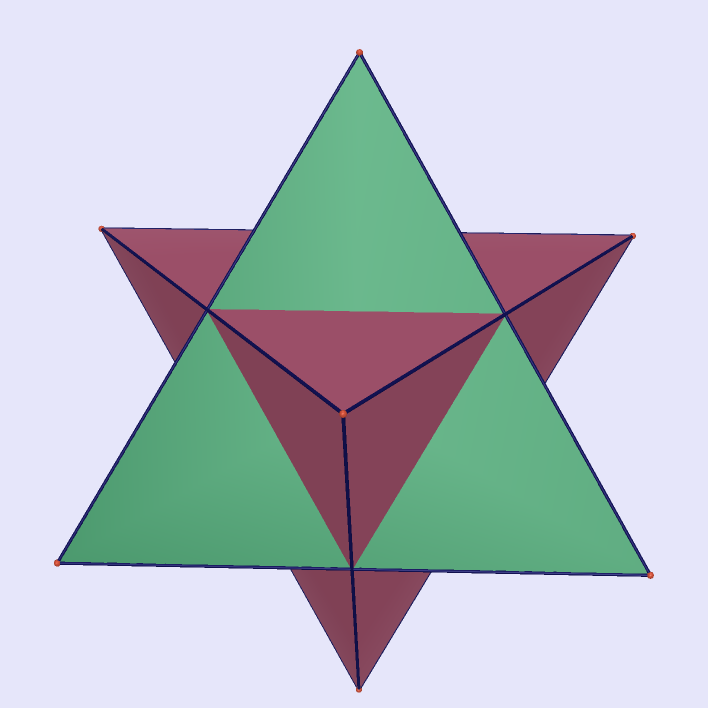
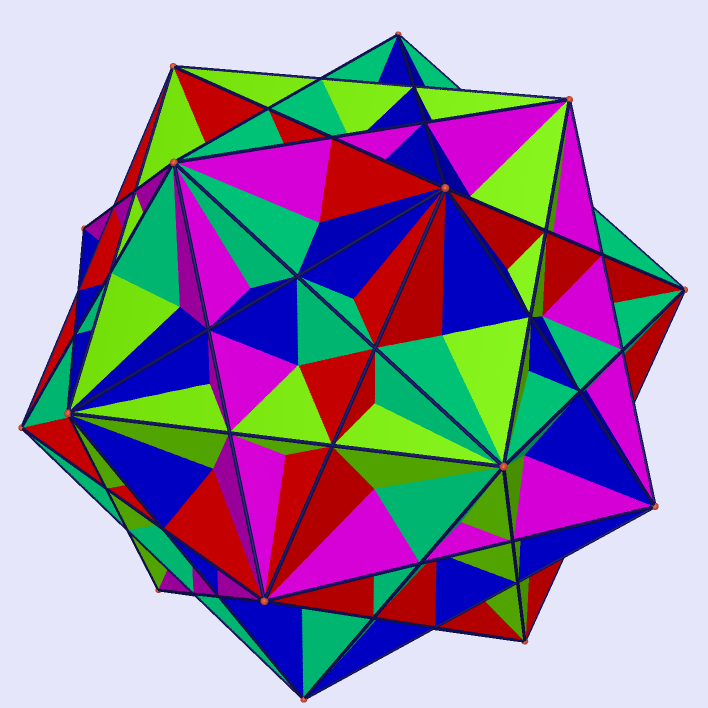
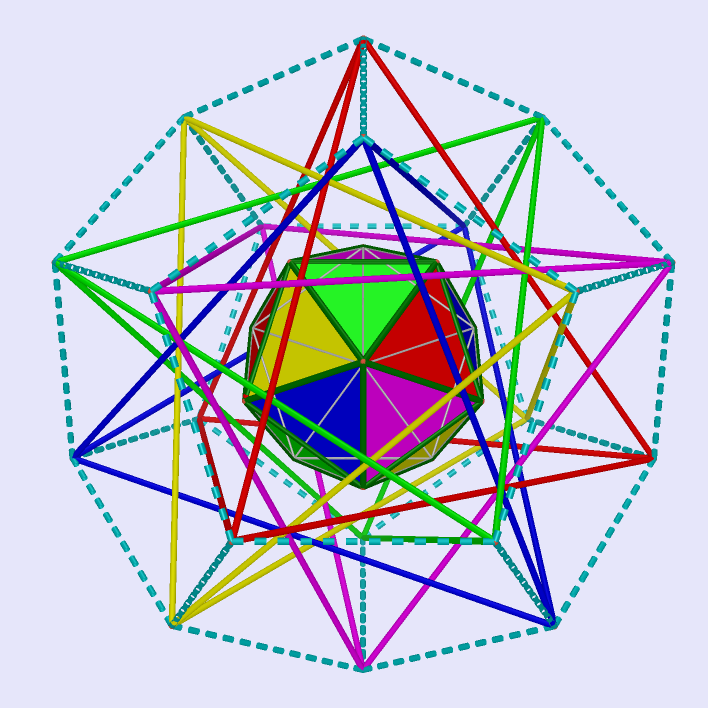
5 Cube inside Regular Dodecahedron		Dual Polyhedron		Regular Icosahedron inside 5 Regular Tetrahedron inside Regular Dodecahedron
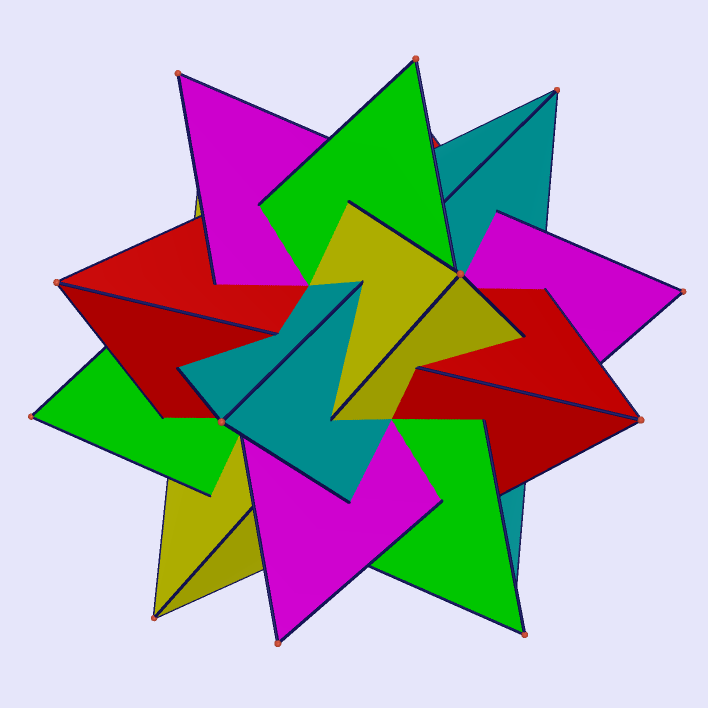
Rhombic Triacontahedron inside 5 Cube inside Regular Dodecahedron		Tetrahedron 5-Compound		The Largest Cubic Contained in Dodecahedron
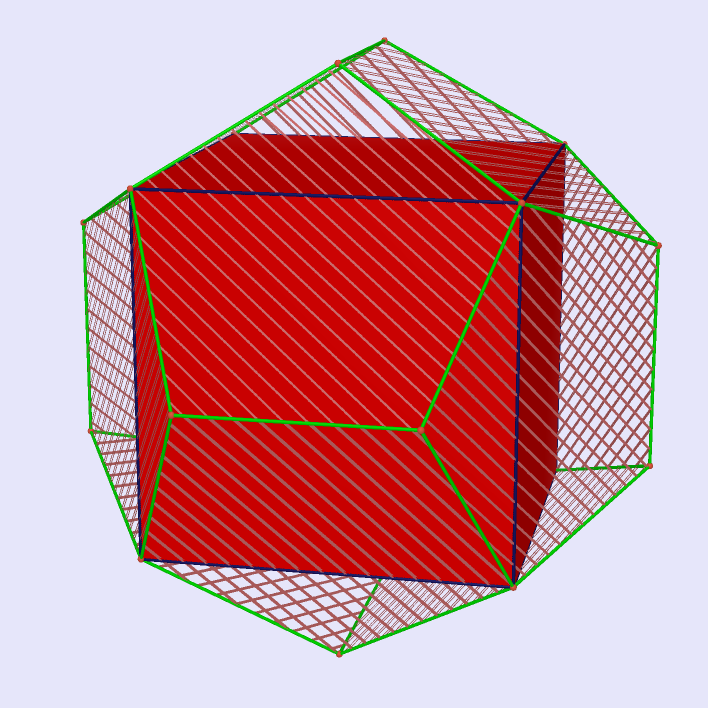
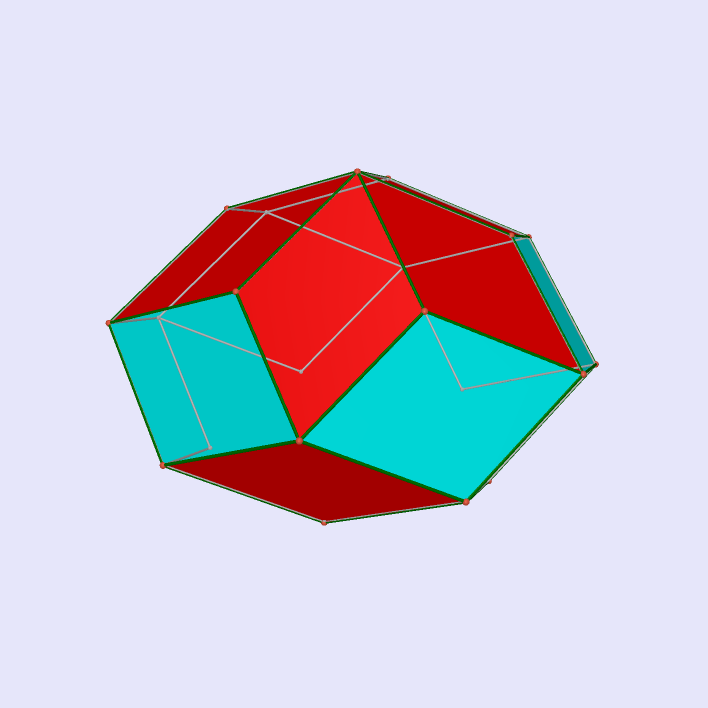
The Largest Icosahedron Contained in Octahedron_		Rhombic Icosahedron		Trigonal Trapezohedron By Half-turn
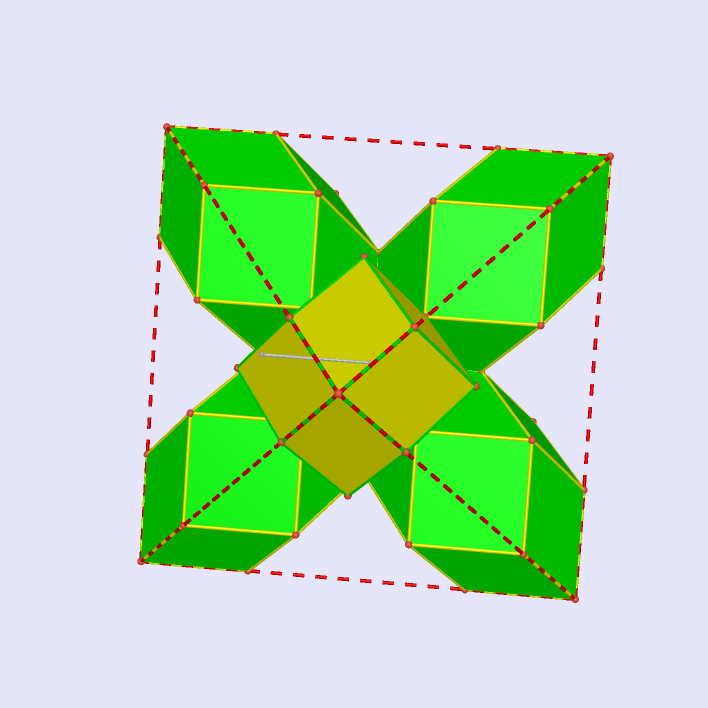
Rhombic Dodecahedron By Half-turn		Animation of Rhombohedron		Animation of Rhombic Dodecahedron
Animation of Rhombic Icosahedron		Animation of Rhombic Polyhedron with 132 Rhombic faces		Rhombic Dodecahedron By Half-sphere
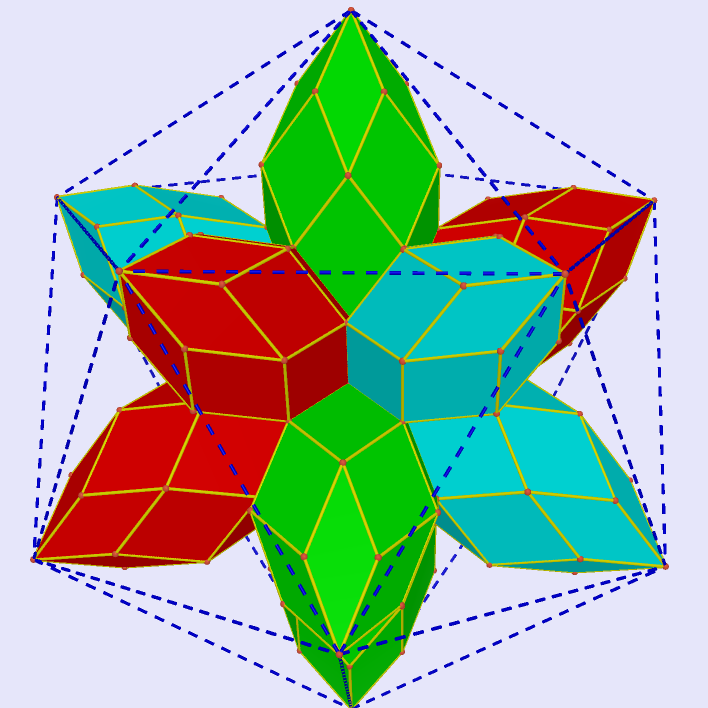
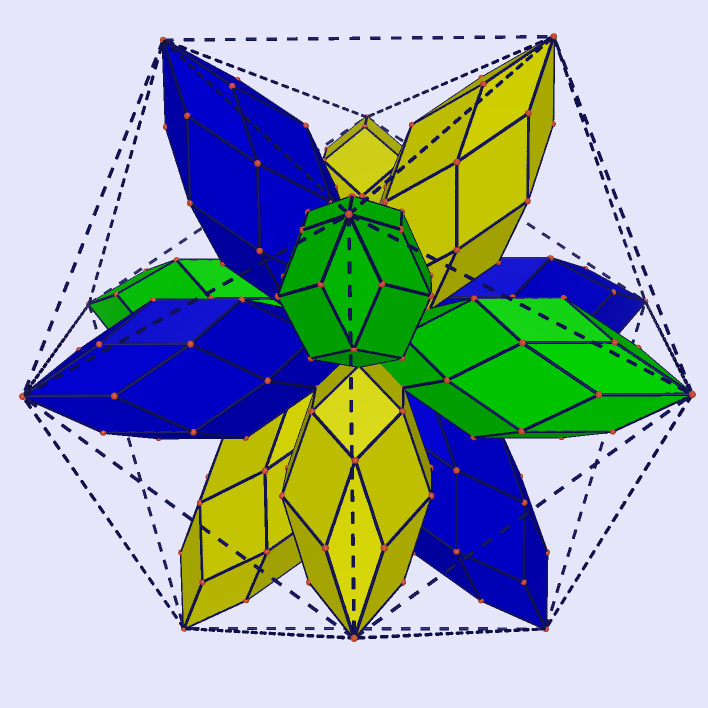
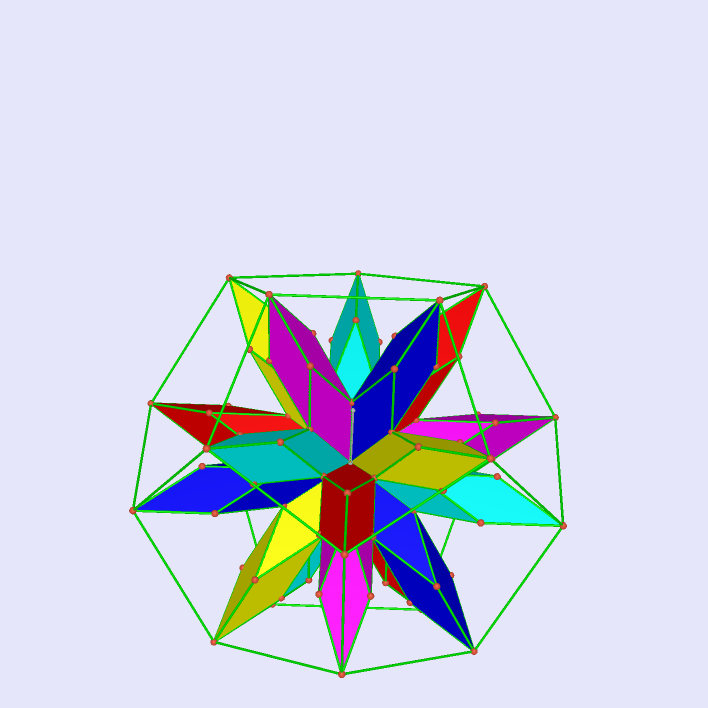
Rhombic Dodecahedrons in Icosahedron		Rhombic Dodecahedrons in Icosahedron		Regular Octahedron Inside Cube
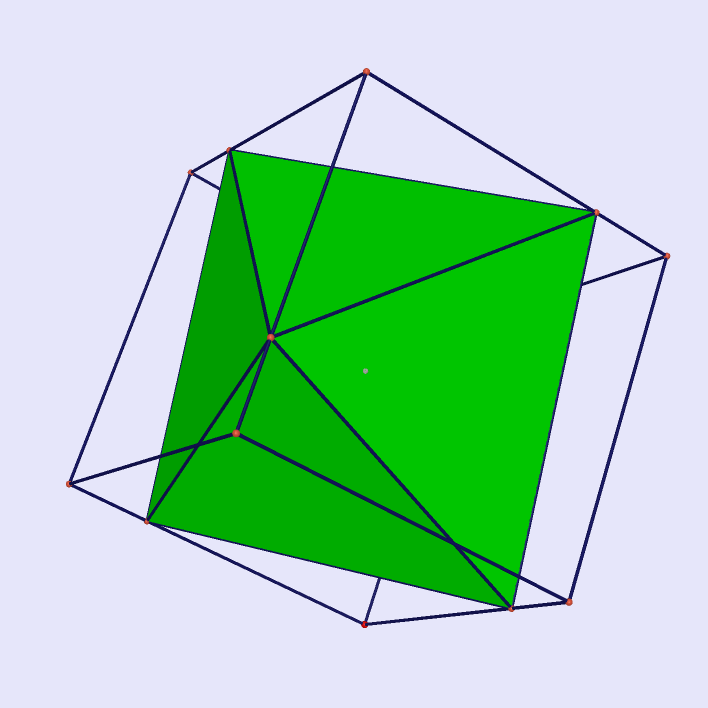
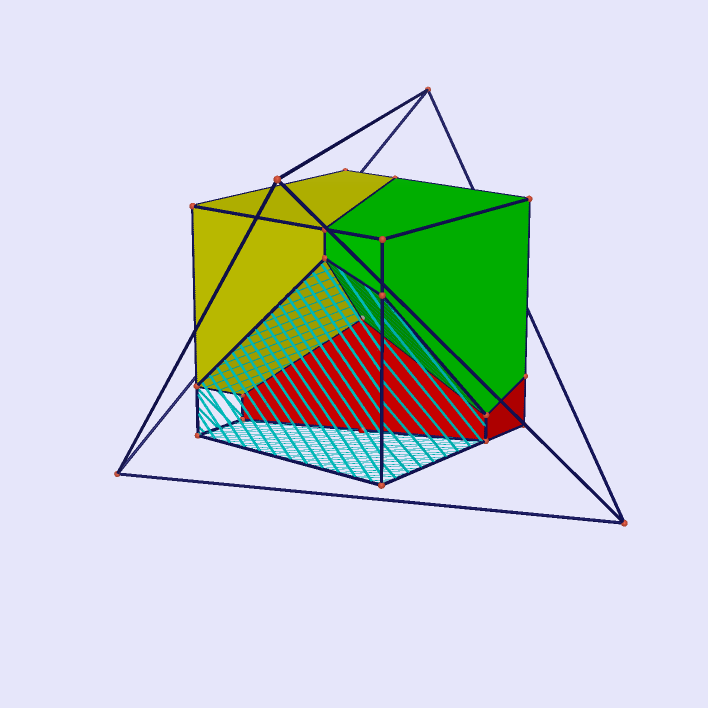
Tetrahedron Projected on Cube		Regular Dodecahedron Inside Cube		Tetrahedron Projected on Regular Tetrahedron
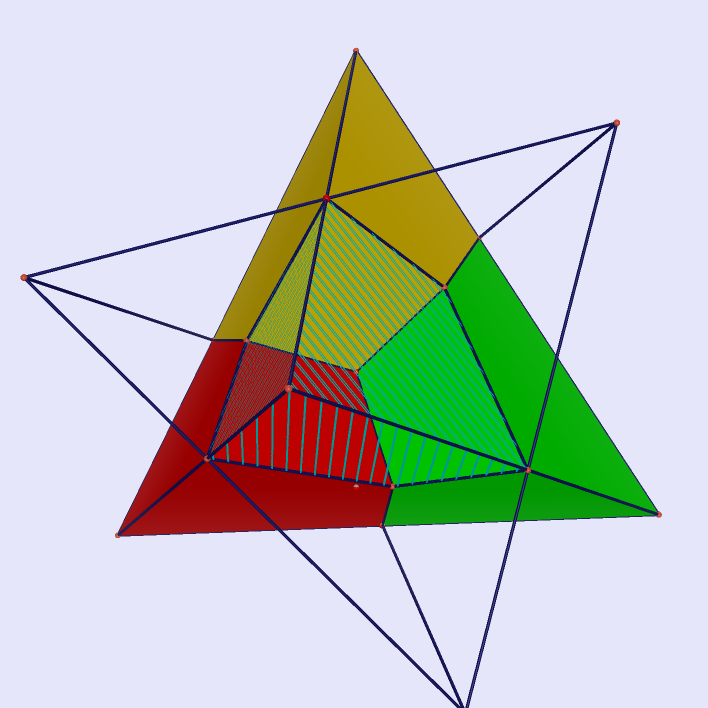
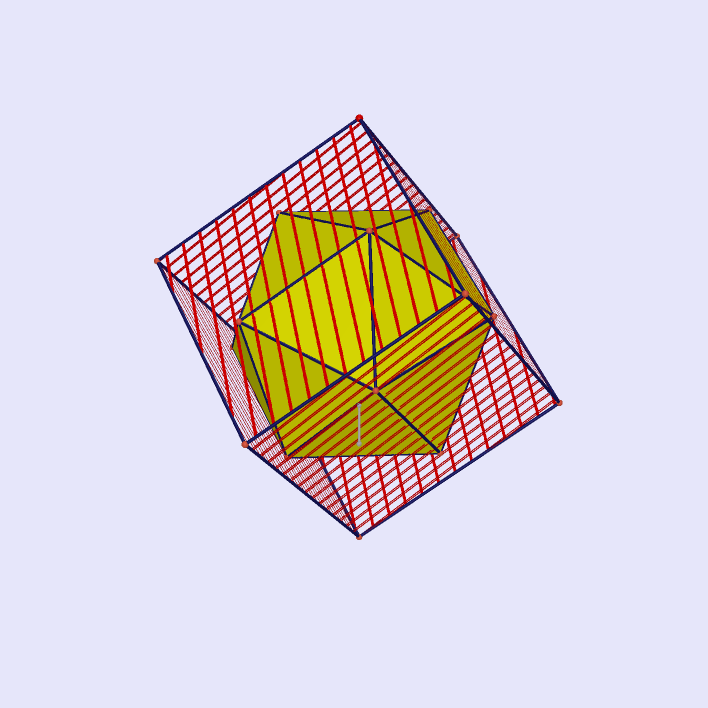
Regular Icosahedron Inside Cube		Continuous Decompositions of a Cube into Six Congruent Parts		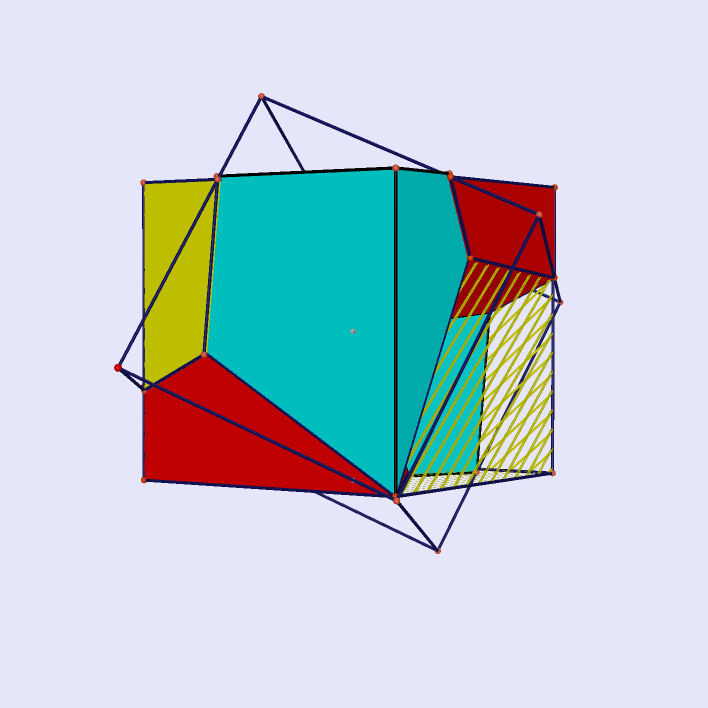Continuous Patterns on Dodecahedron Projected by the Cube
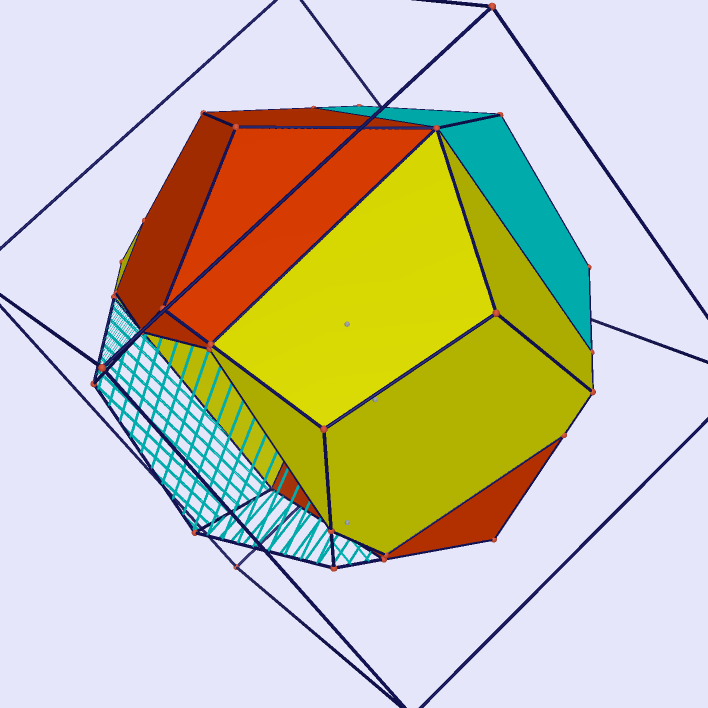Rotating Cube Projected on the Octahedron		Deltoidal Hexecontahedron		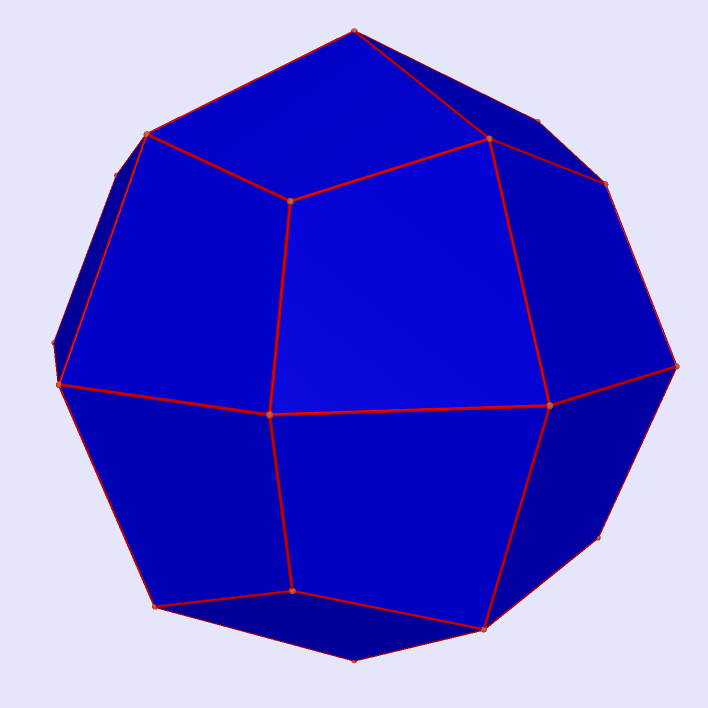Great Rhombicosid -odecahedron
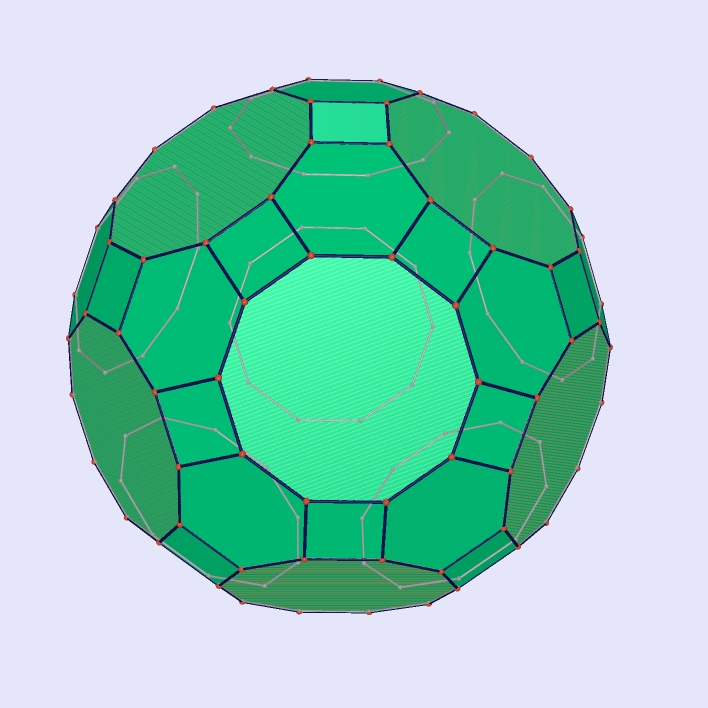Great Rhombicuboctahedron		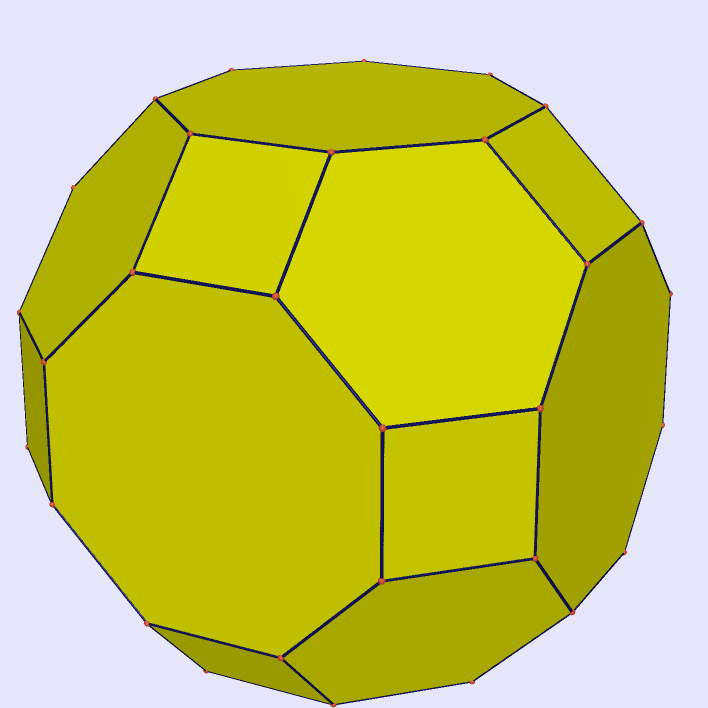small rhombicuboctahedron		Triangular orthobicupola
Small Rhombicosidodecahedron		Deltoidal Icositetrahedron		Pentagonal Icositetrahedron
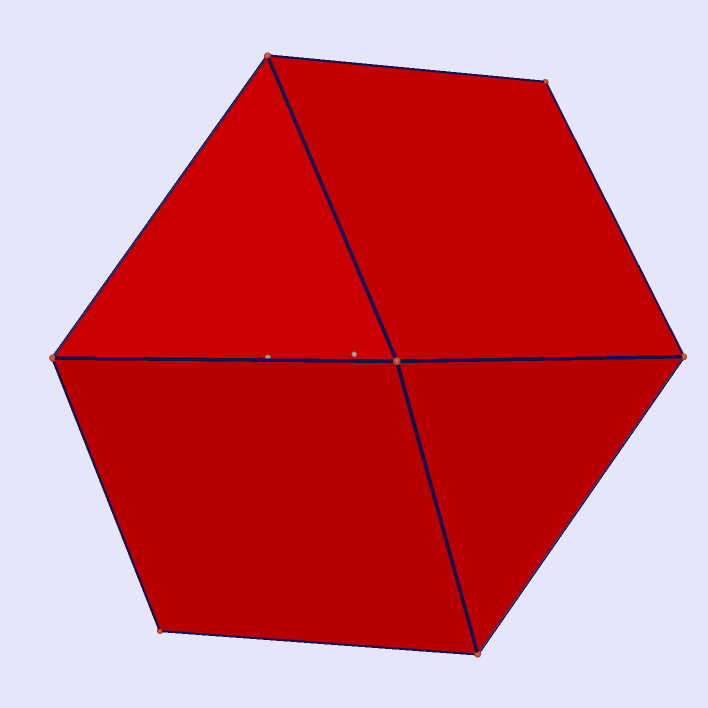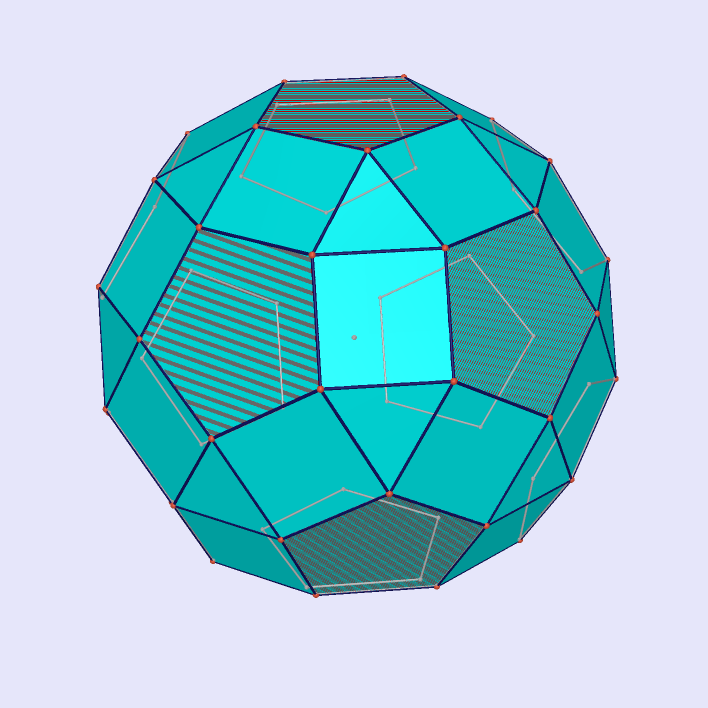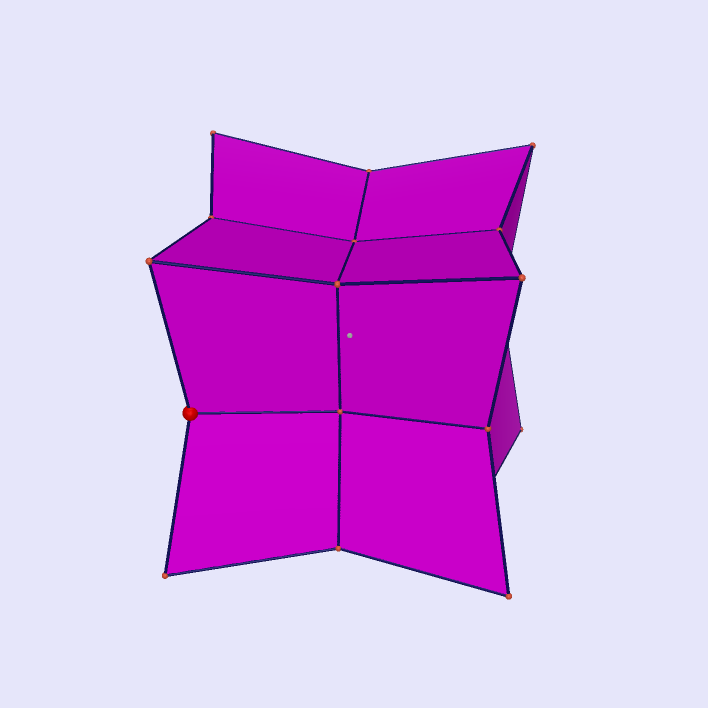Cube Projected on Regular Dodecahedron		Tetrahedron Projected on Regular Dodecahedron		Tetrahedron Projected on Tetrahedron
Tetrahedron Projected on Cube		Cube inside Regular Dodecahedron		Regular Dodecahedron inside Cube
Octahedron inside Cube		Rhombic Triacontahedron inside Cube
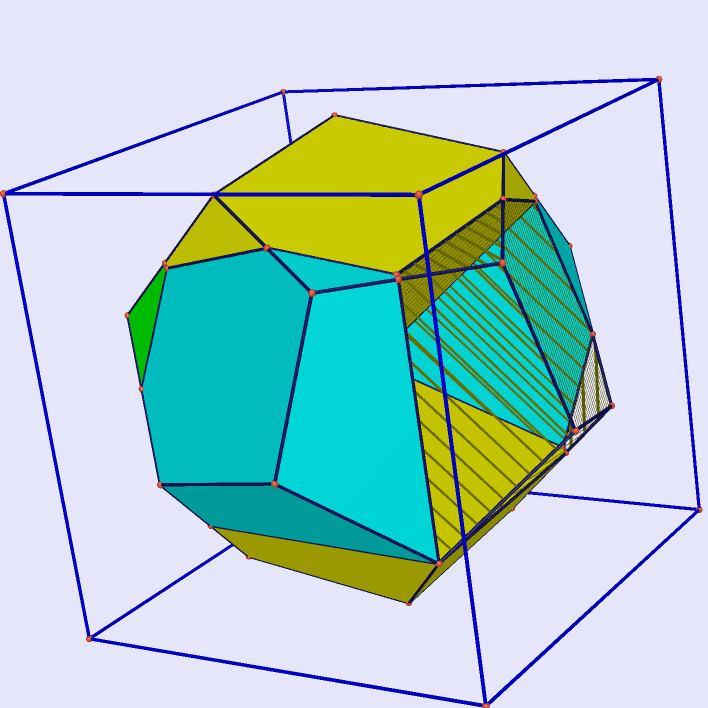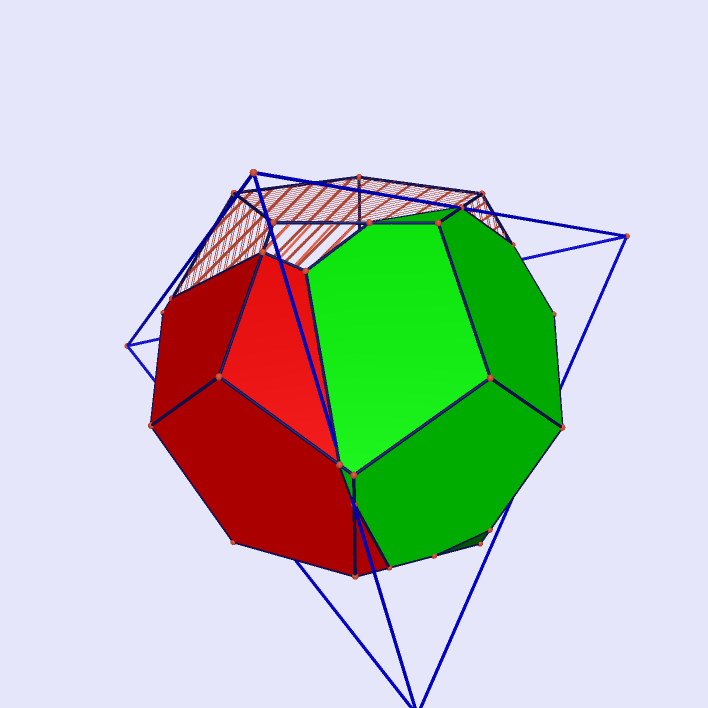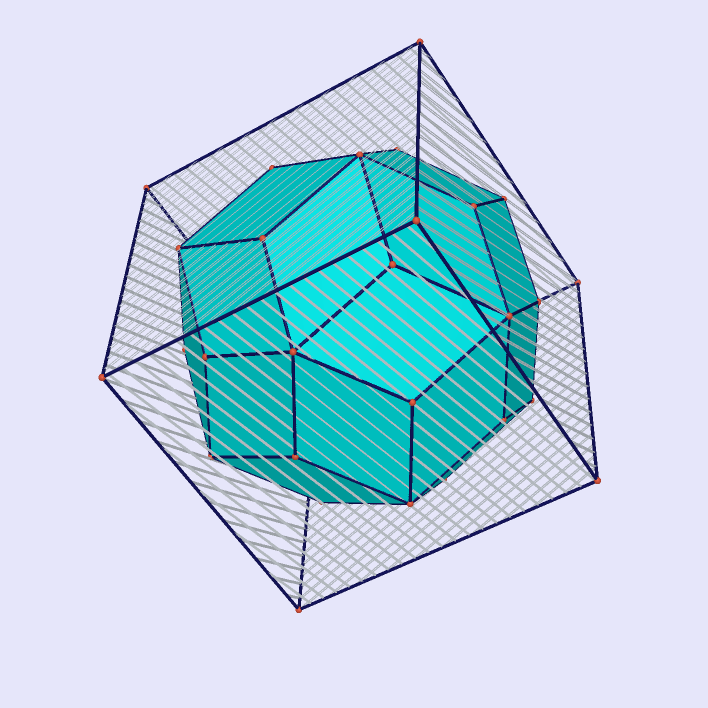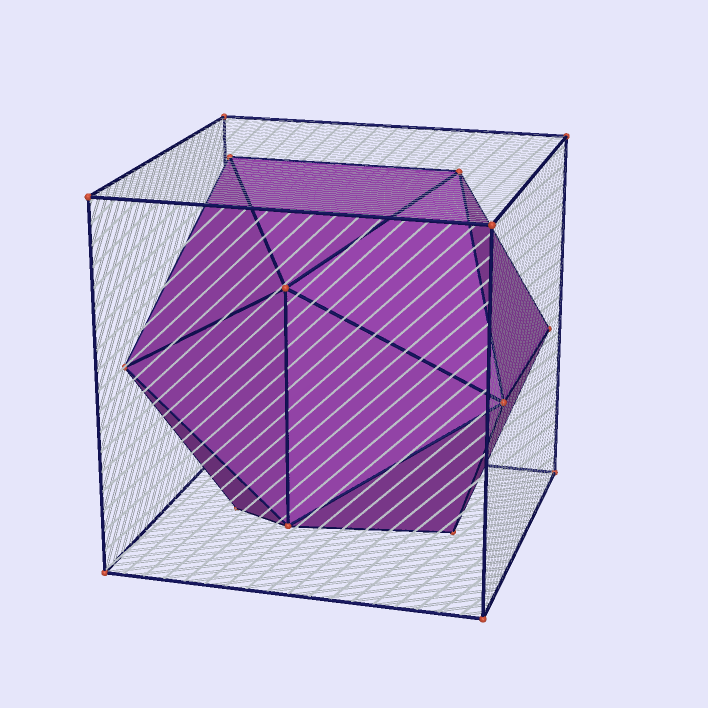Regular Icosahedron inside Cube		Buckyball as Intersection of Dodecahedron with Icosahedron
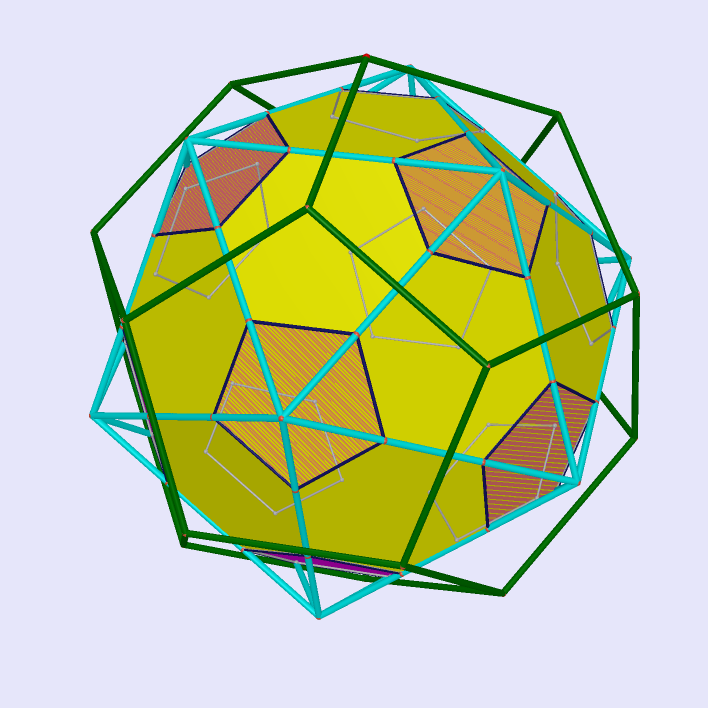
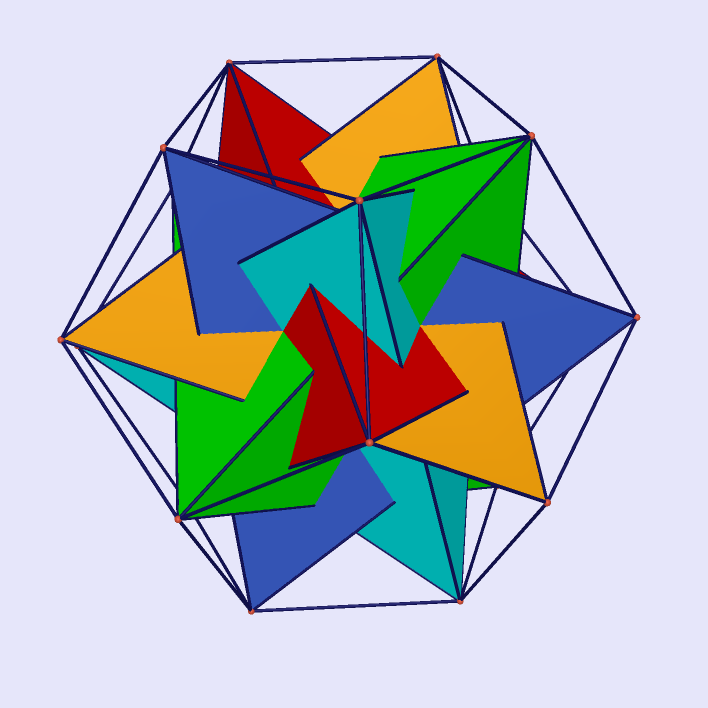
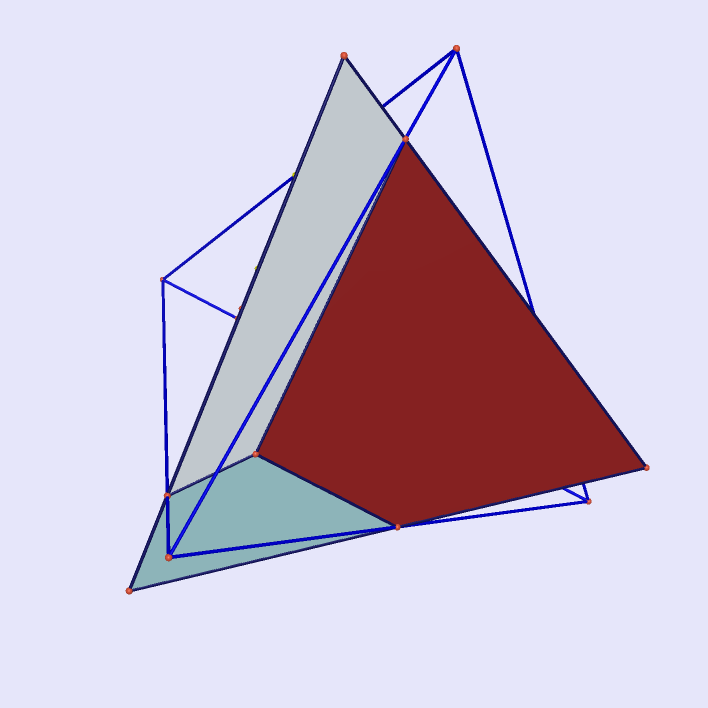
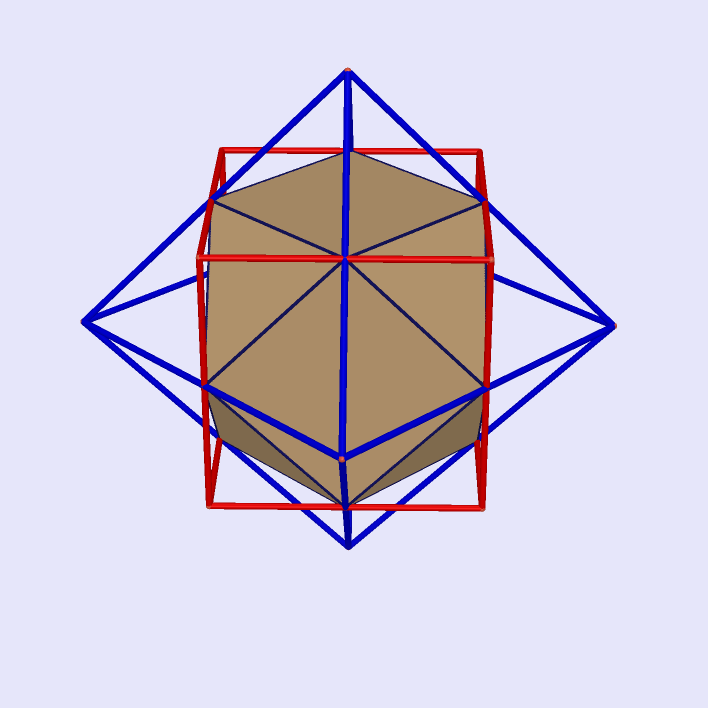
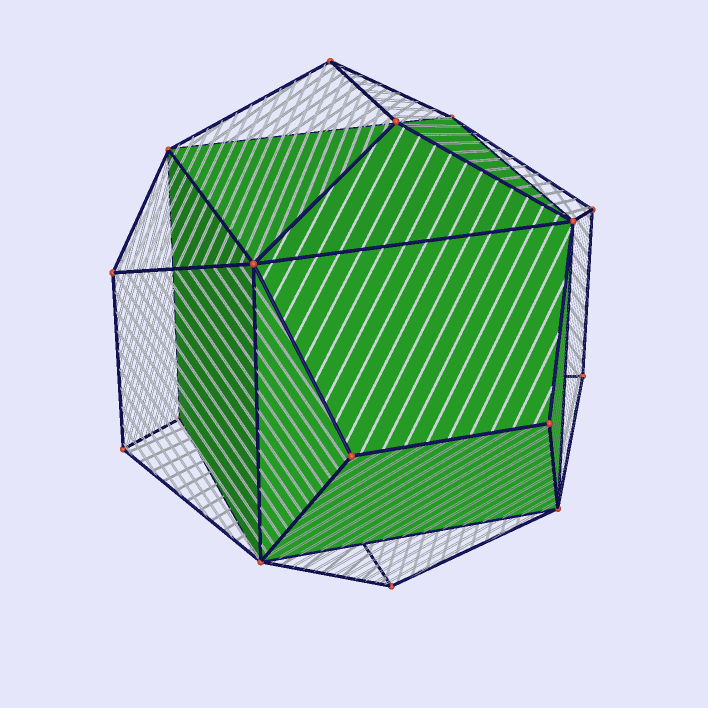
Compound of Five Tetrahedra		Cube and Regular Tetrahedron Intersecting at Cuboctahedron		Deltoidal Icositetrahedron as Intersection of Rhombic Hexahedrons
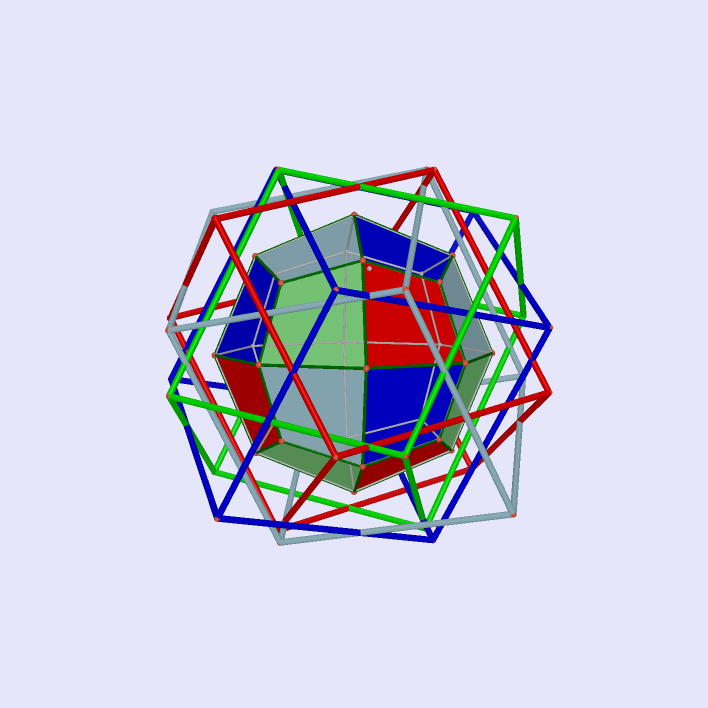
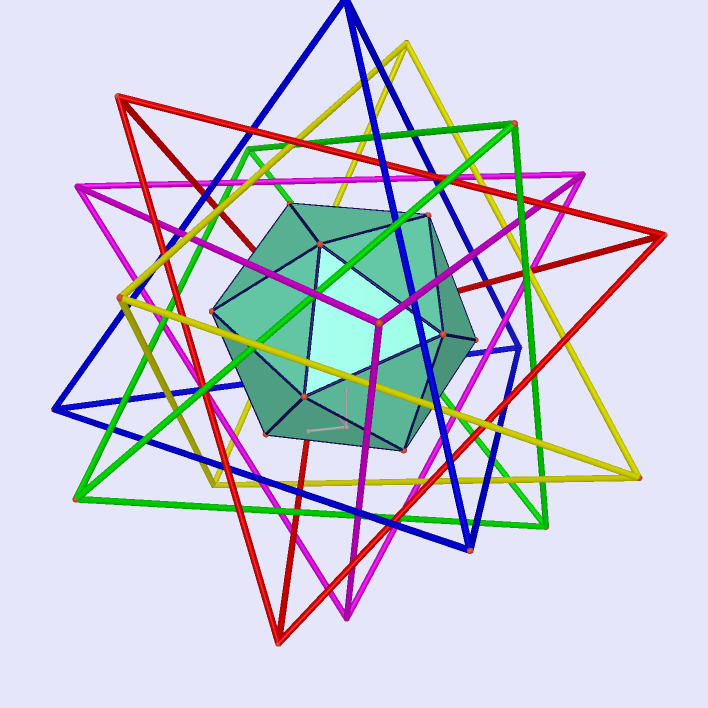
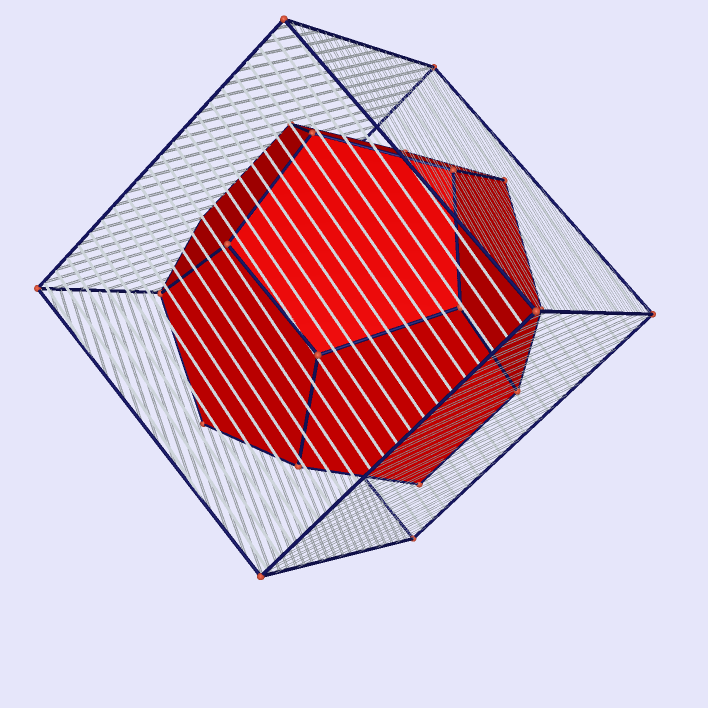
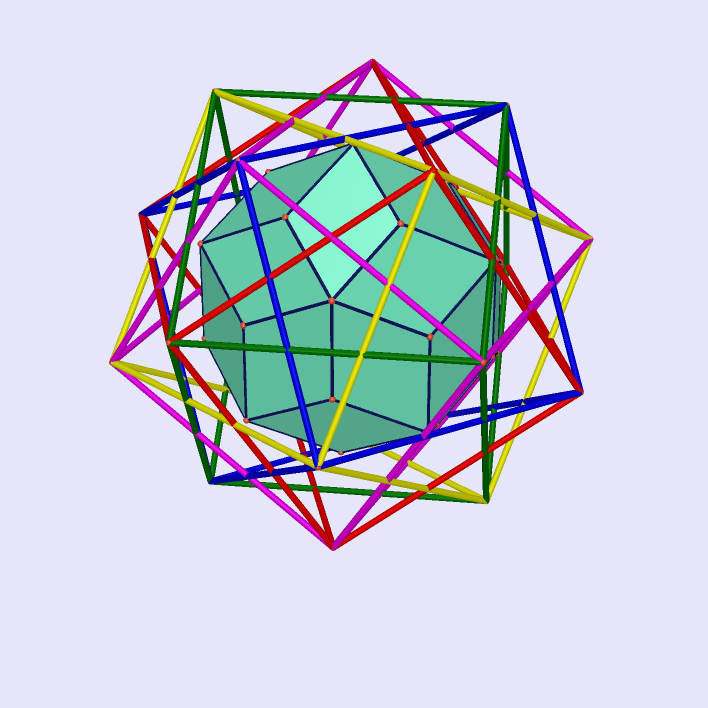
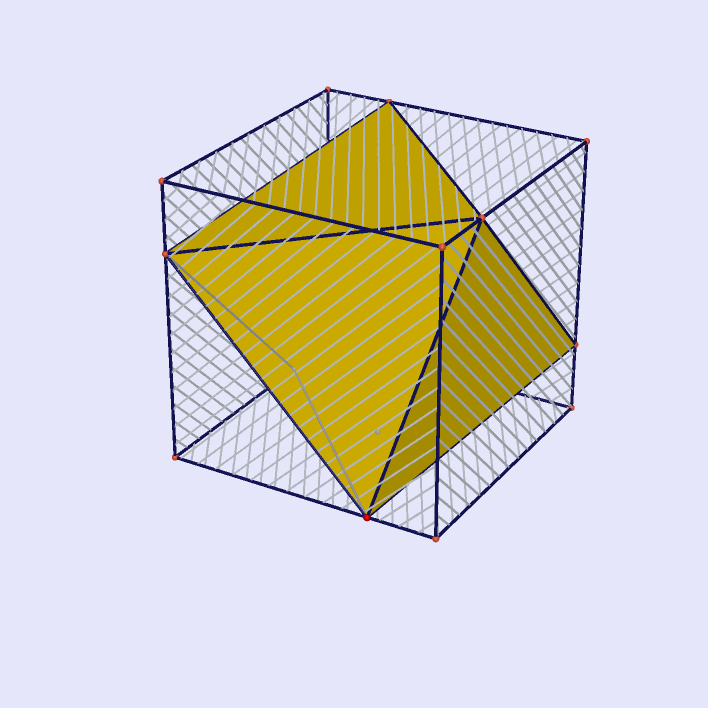
Faces of Icosahedron lie on Faces of Five Tetrahedra		Five Cubes with Rhombic Triacontahedron as Intersection		Five Octahedra Intersecting at Icosahedron
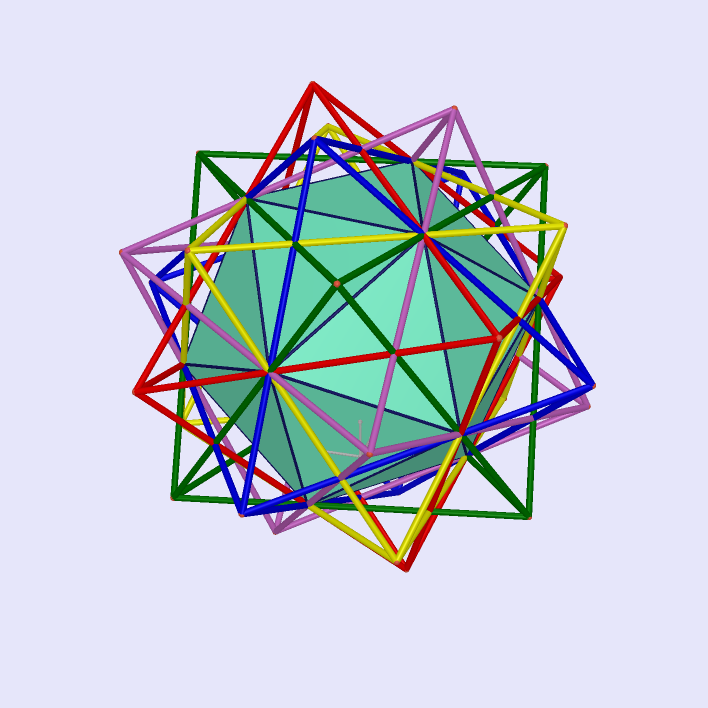
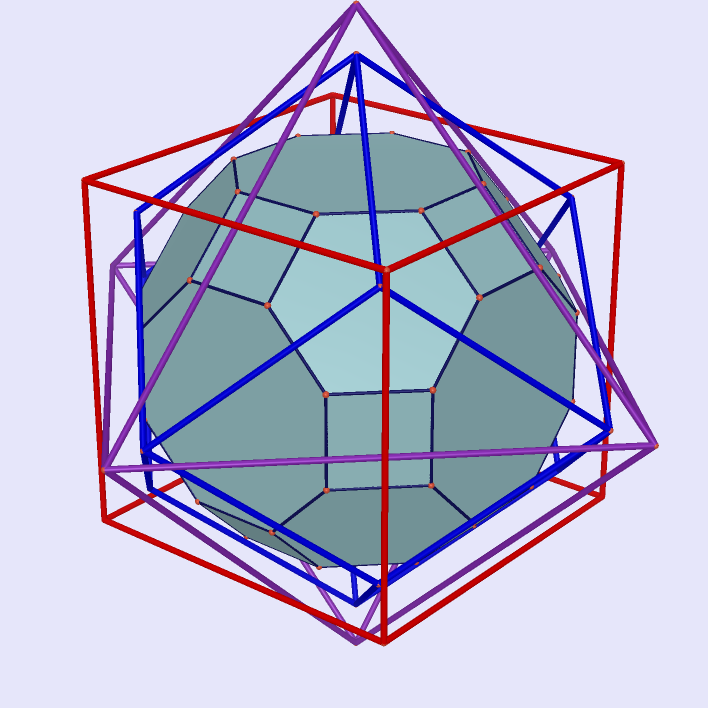
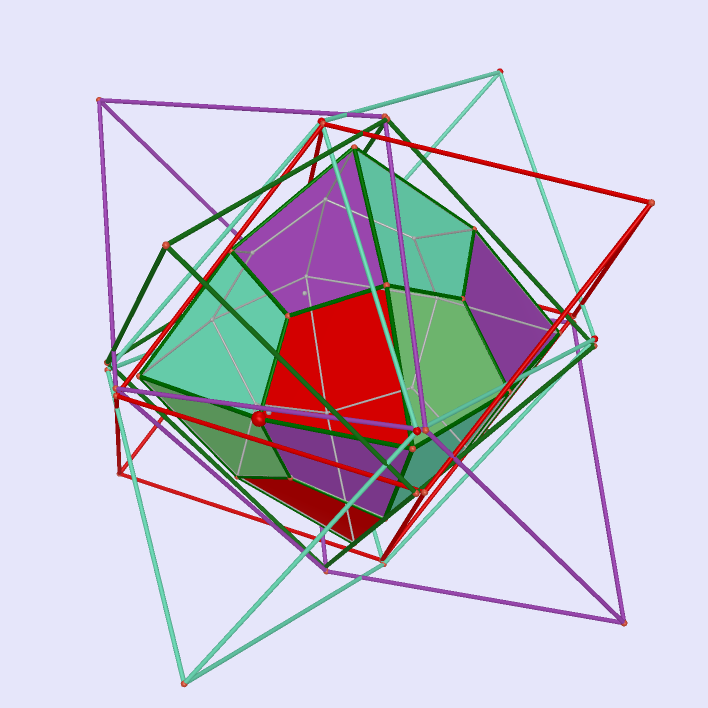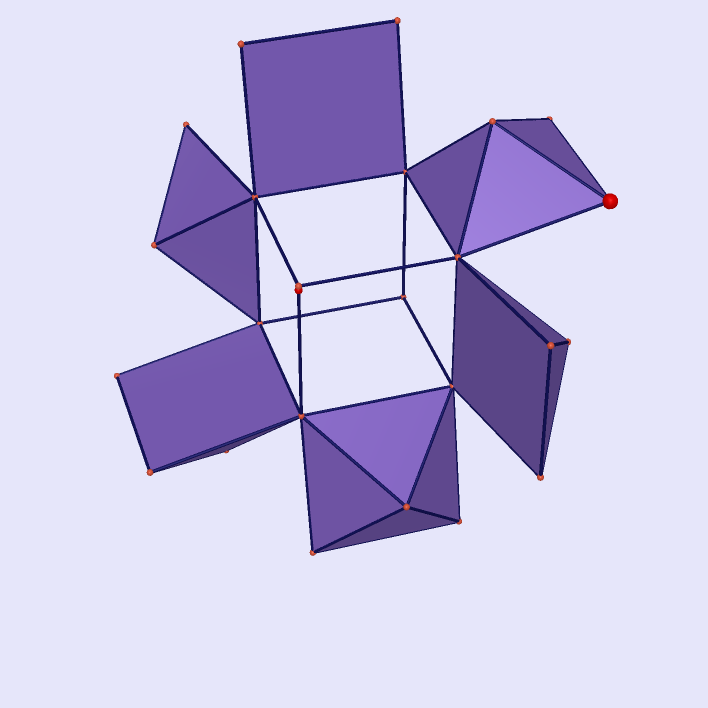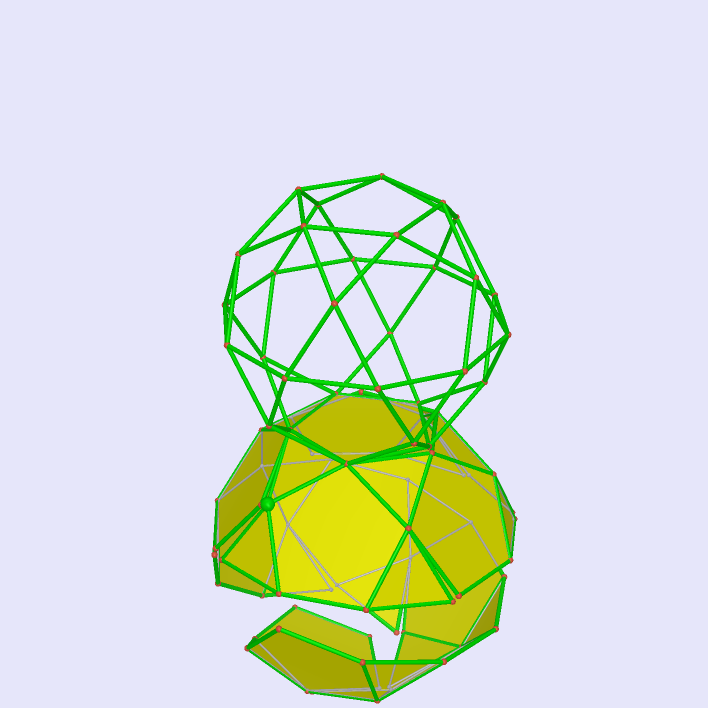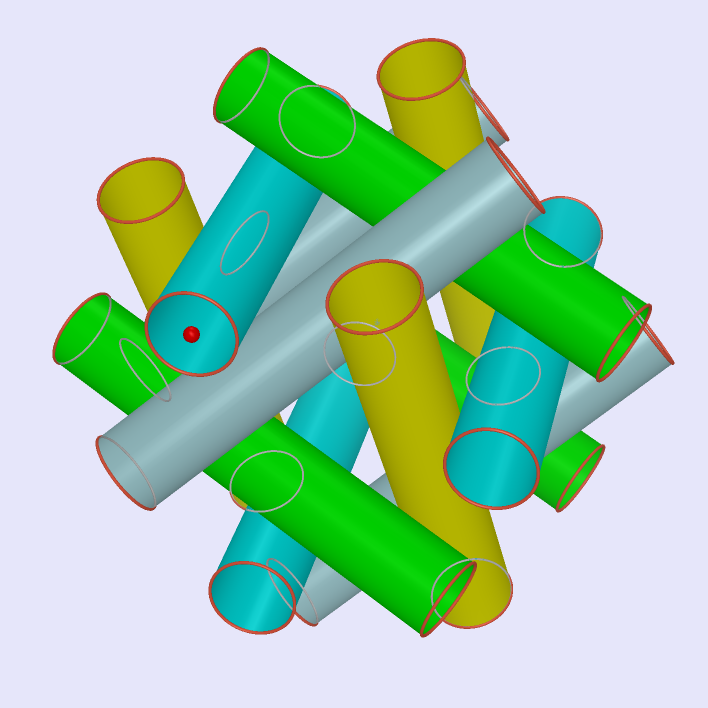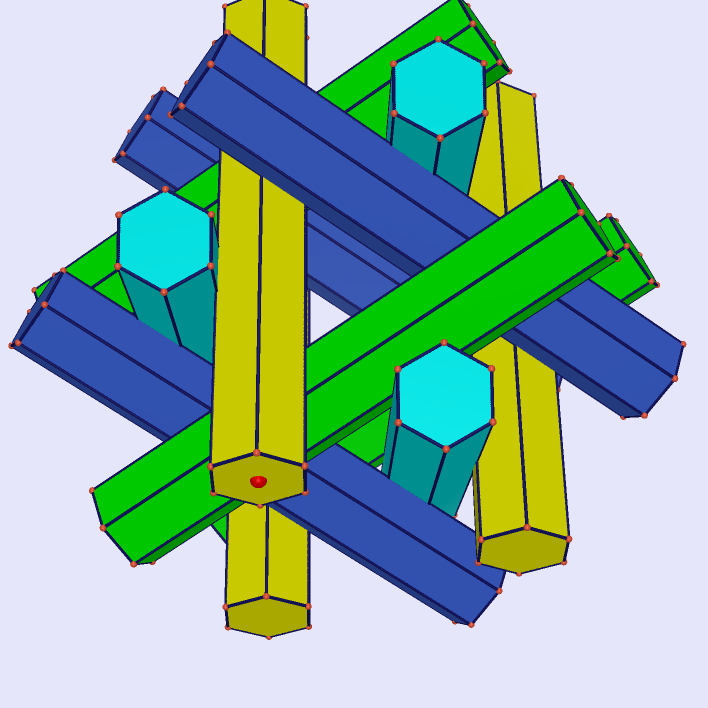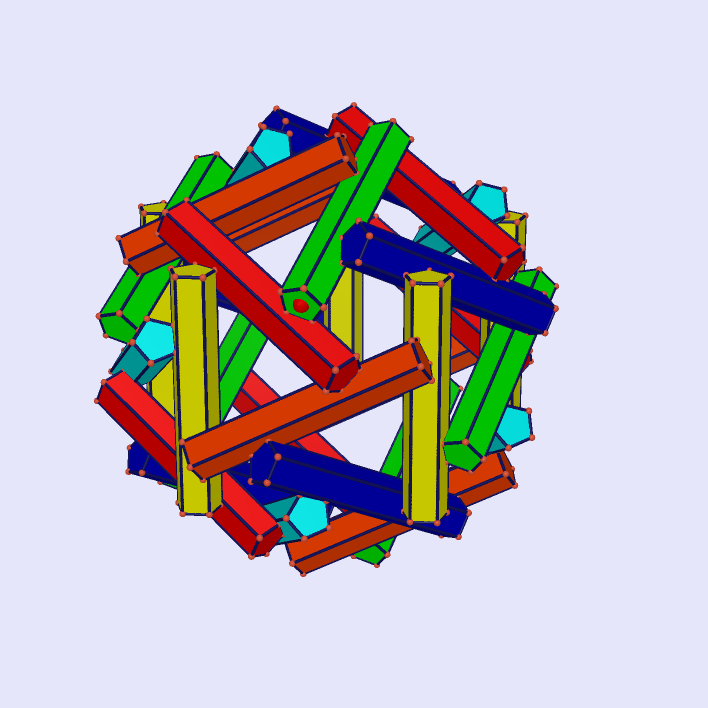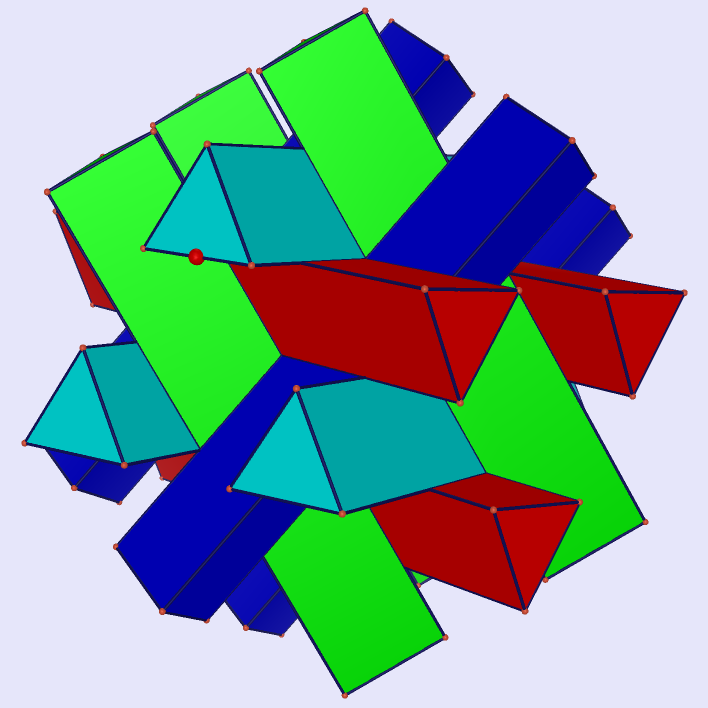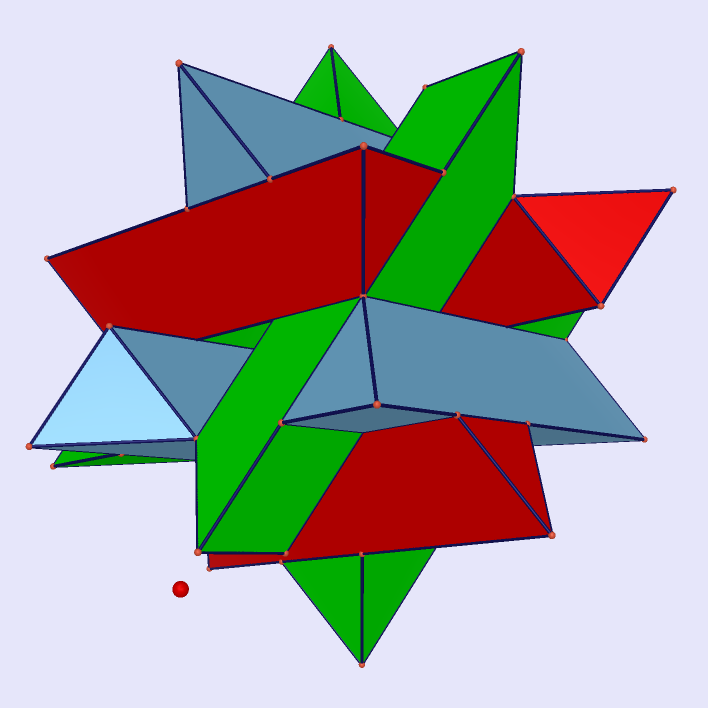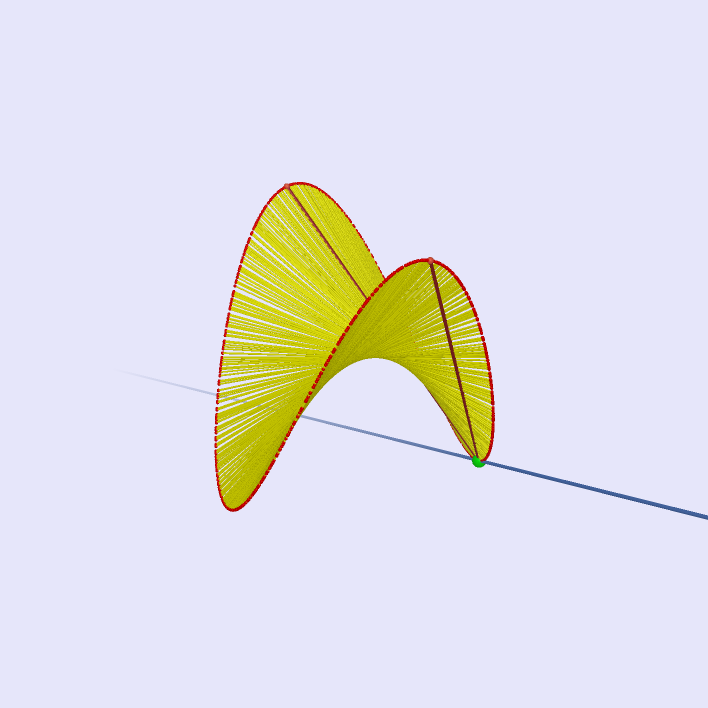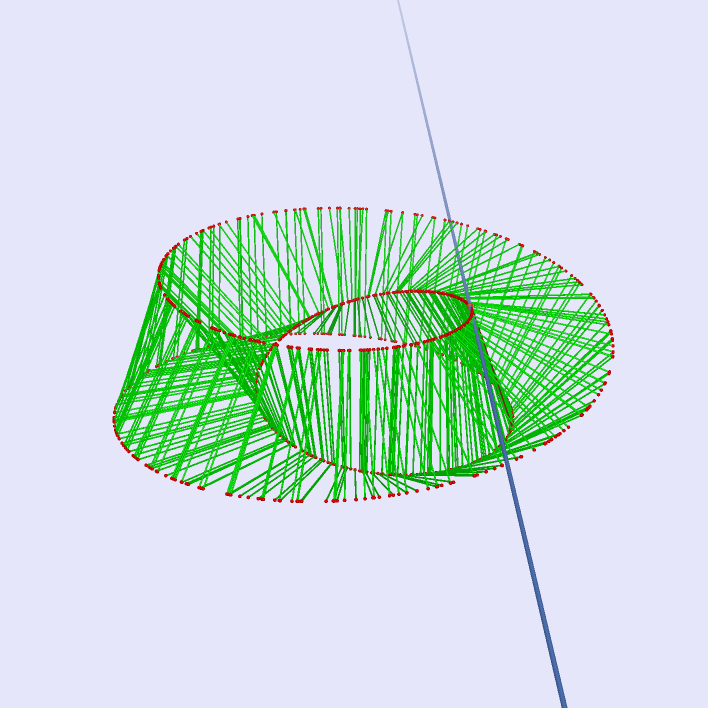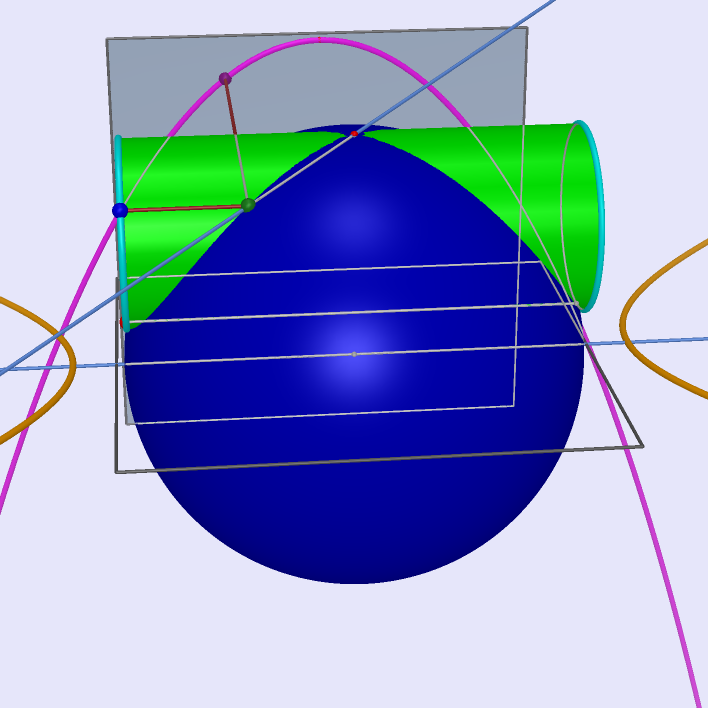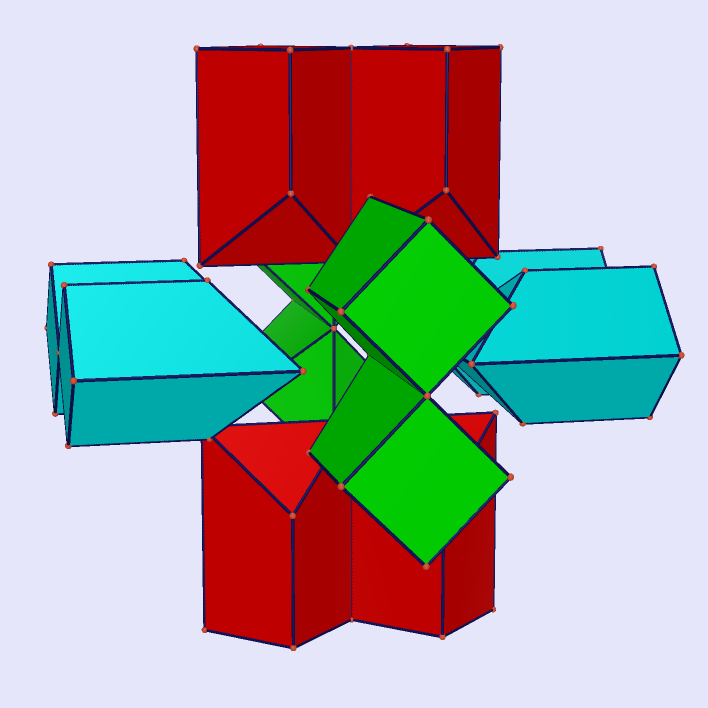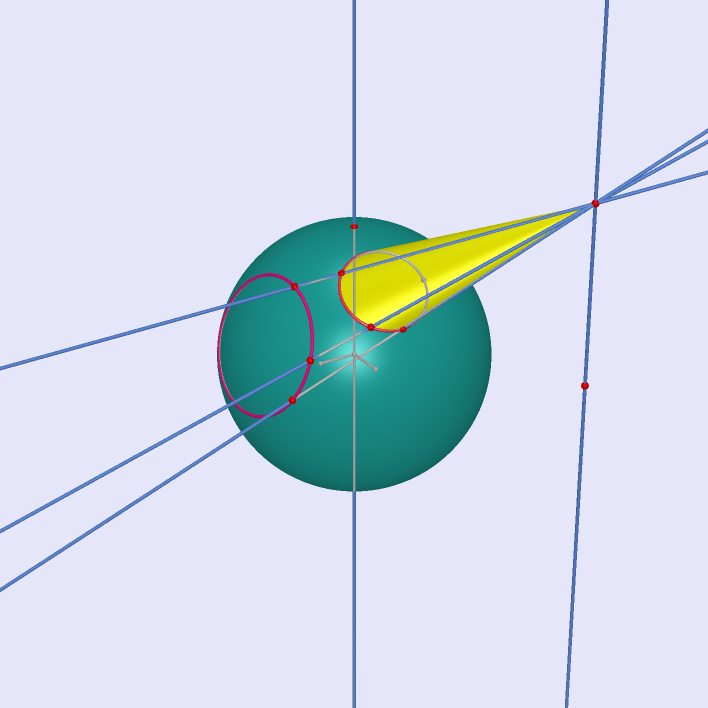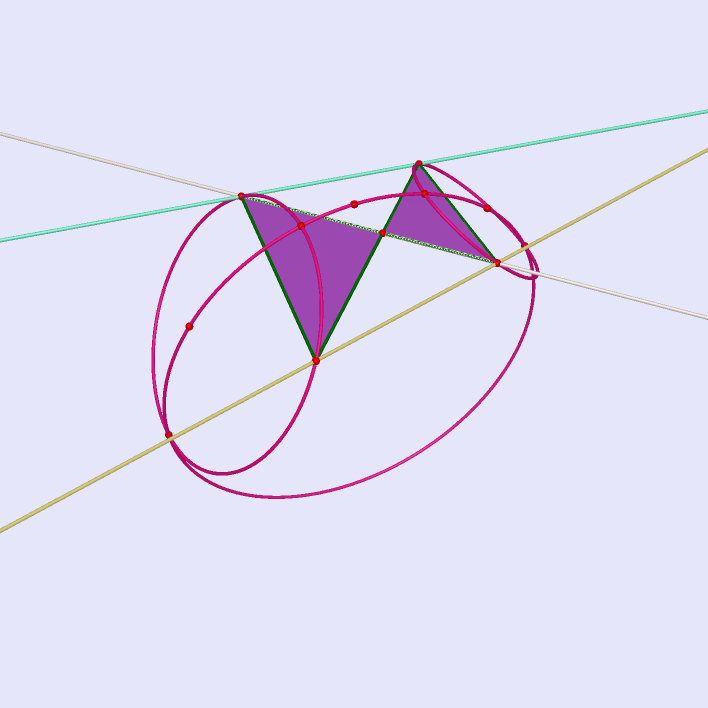Great Rhombicuboctahedron as Intersection of Rhombic Dodecahedron, Octahedron and Cube		Tetrated dodecahedron as Intersection of Dodecahedron with Icosahedron		Deltoidal Icositetrahedron as Intersection of Rhombic Hexahedrons
Magic of Cube		Cube-Rhombic Dodecahedron		Open of Dodecahedron
Open of Cube		Dodecahedron Hexecontahedron		Open of Tetrated Dodecahedron
12 Cylinder in Tight Formation		12 Pencils in Tight Formation		30 Cylinder in Tight Formation
30 Pencils in Tight Formation		12 Triangular Prism in Tight Formation		Broken Sticks Puzzle
Hyperbolic Paraboloid		Torus		Triangle Mobius
Half of Torus		Hyperbolic Paraboloid and Tangent		Triangle Mobius and Tangent
Conic Section Curve as a Projection		Steinmetz Solid		Region Enclosed By Two Parabolic Cylinders
Stellation of Rhombic Dodecahedron Formed with Six Unlock Burrs		Inverse circle on sphere 2		Inverse circle on sphere 3
Inverse circle on sphere 1		Stellation of Rhombic Dodecahedron Formed with Six Burrs