幾何作圖

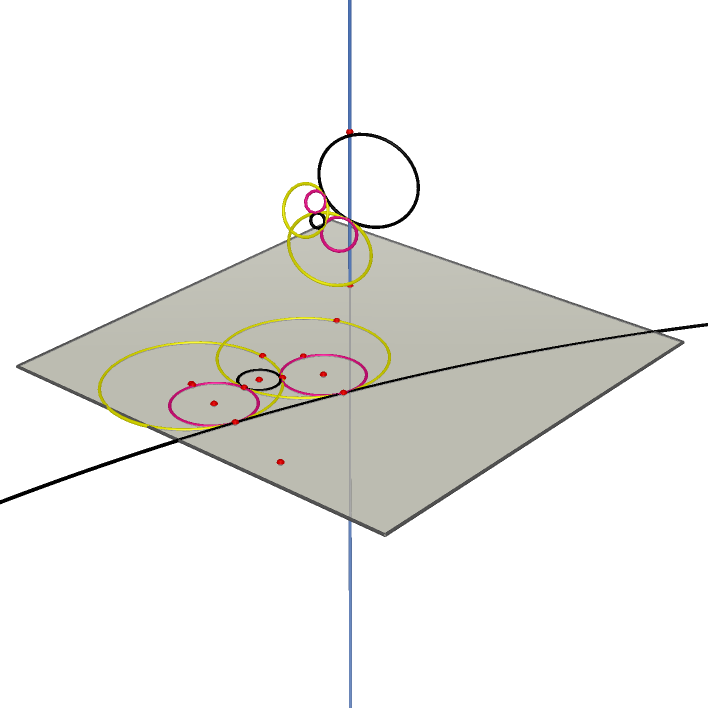
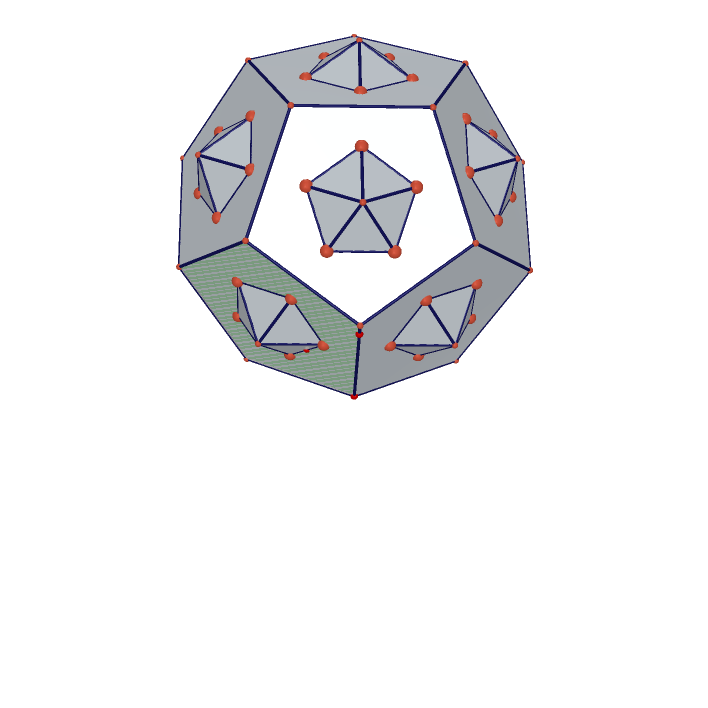
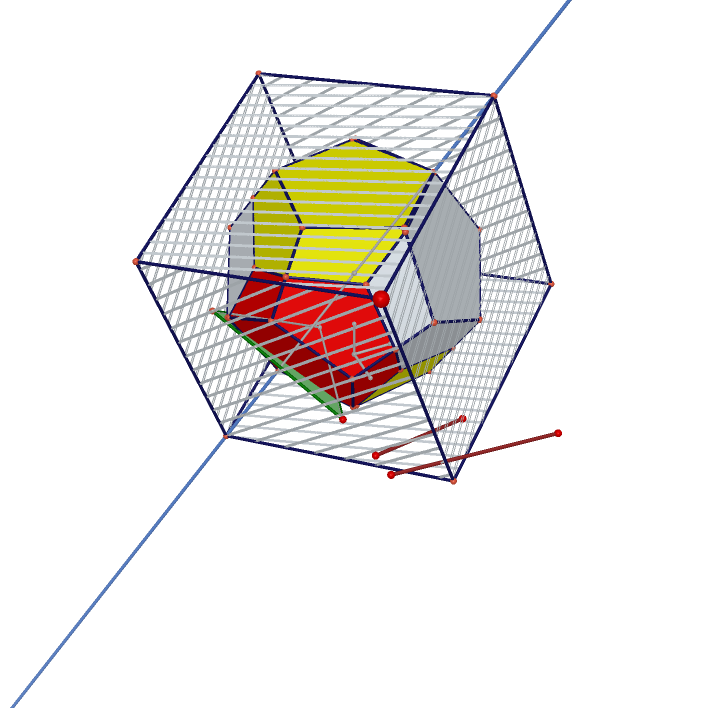
12 Tangent Circles (Inverse by Dodecahedron)	12 Tangent Circles (Inverse by Pentagonal Cupola)	20 Rhomboic Polyhedral In Regular Dodecahedron	24 Tangent Circles (Inverse by Deltoidal Icositetrahedron)	26 Tangent Circles (Inverse by Truncated Cuboctahedron)	3 Orthogonal Rectangle In Regular Dodecahedron	4 Tangent Circles on Sphere	5 Cube inside Regular Dodecahedron	6 Tetrahedron In Dodecahedron

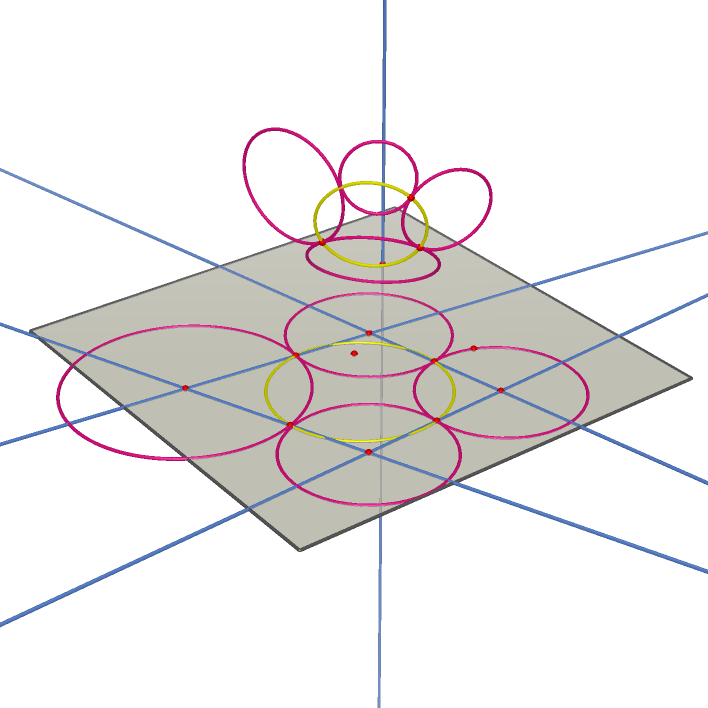
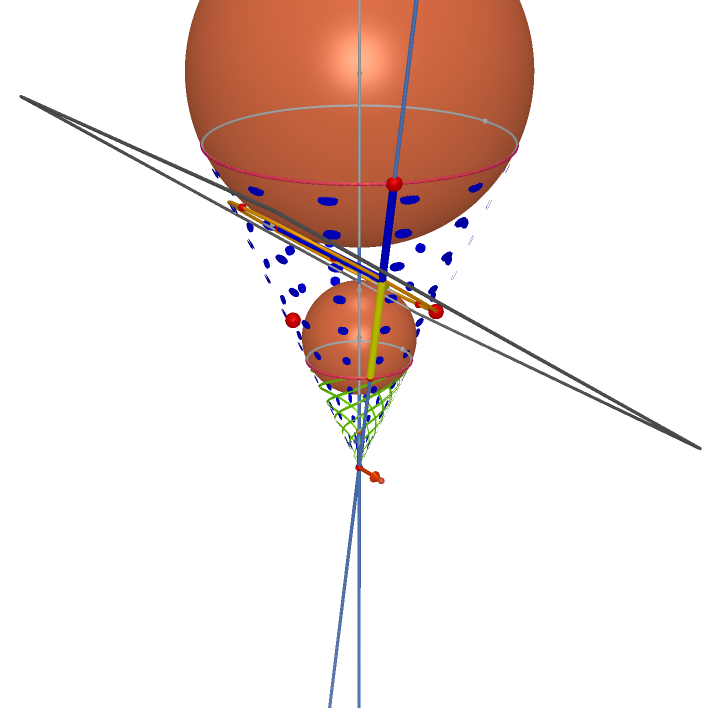
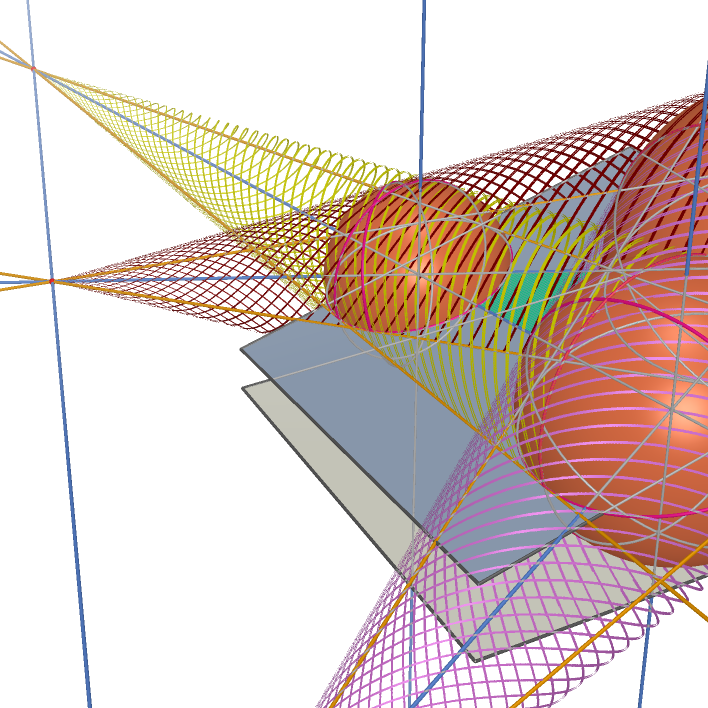
8 Tangent Circles (Inverse by Octahedron)	8 Tangent Circles on Sphere (Inverse by Octahedron)	8 Tangent Circles on Sphere (Inverse by Triangular Cupola)	A Chain of Four Circles Each Tangent to Two Fixed Intersection Circles	A Circle Though 4 Tangent Point of 4 Circles on Sphere	A Ellipse in 3-Dimensional Space	Bucky Ball as Intersection of Dodecahedron and Icosahedron	Common Tangent Cones of Three Spheres

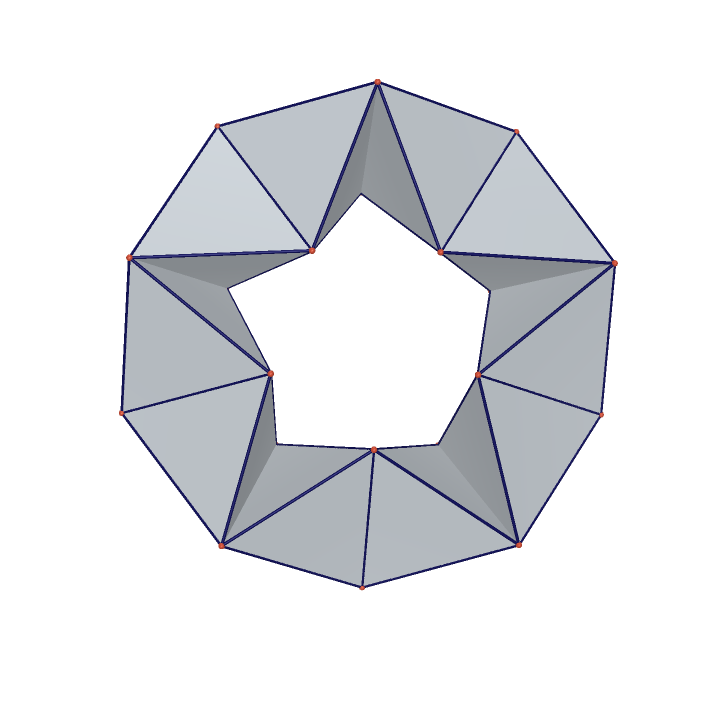
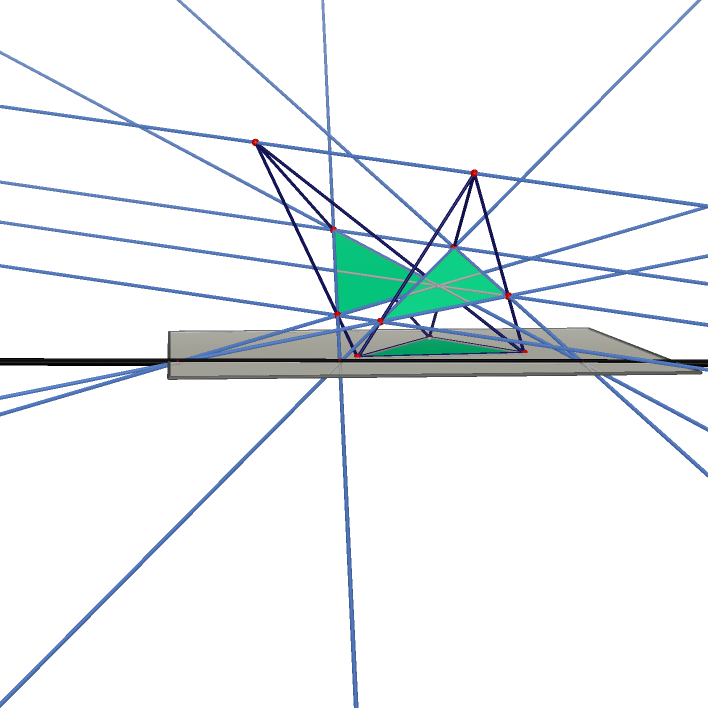
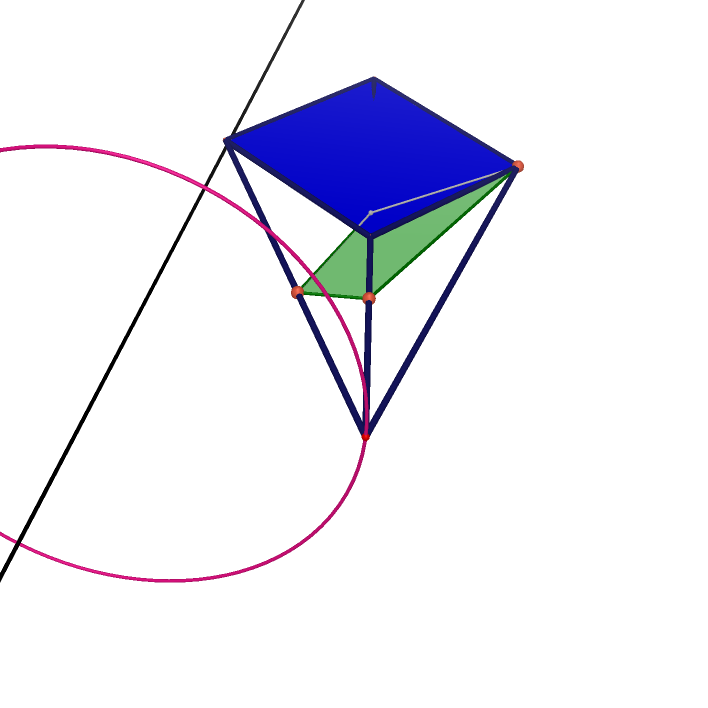
Concave 120-faced Rhombic Polyhedra	Concave 60-faced Rhombic Polyhedra	Continuous Patterns on Dodecahedron Projected by the Cube	Deltoidal Icositetrahedron	Desargues' Theorem with Two Triangle in Different Tetrahedron	Desargues' Theorem with Two Triangle in the Same Tetrahedron

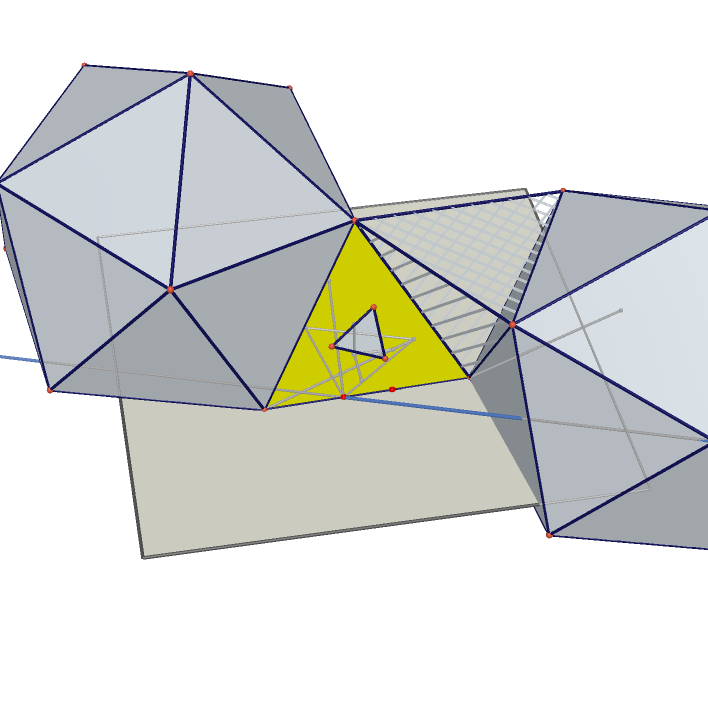
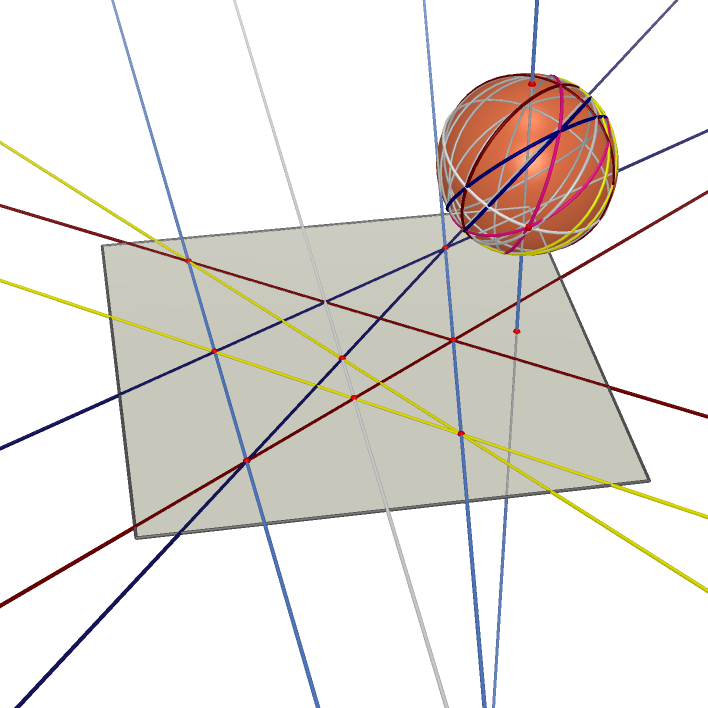
Great Ditrigonal Icosidodecahedron	Inspired by Paper Folding	Jitterbug	Kaleidocycles-5	Largest Icosahedron Inside a Tetrahedron	Pappus's Hexagon Theorem on Sphere

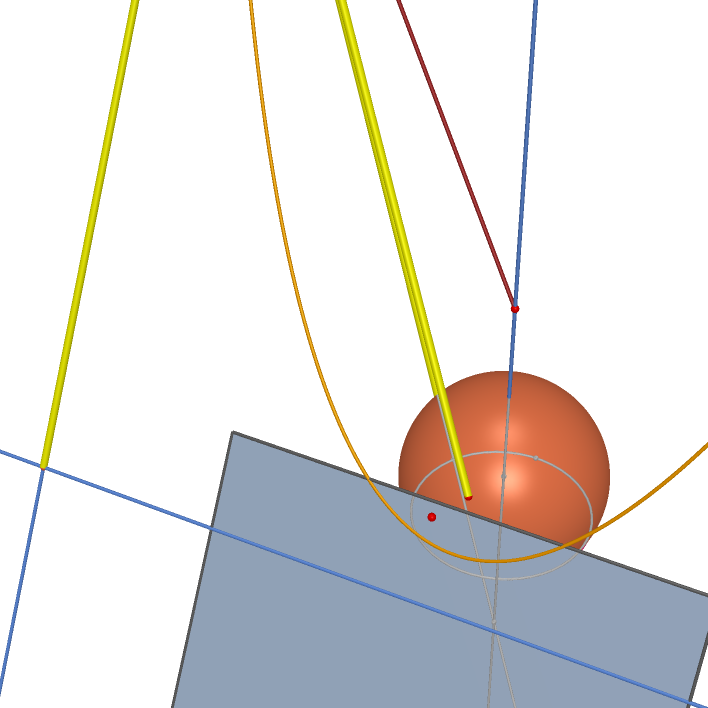
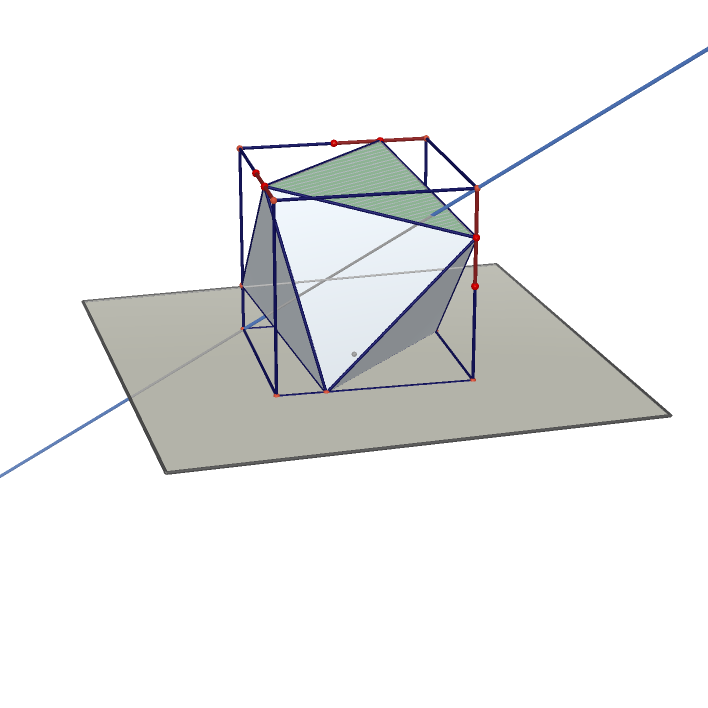
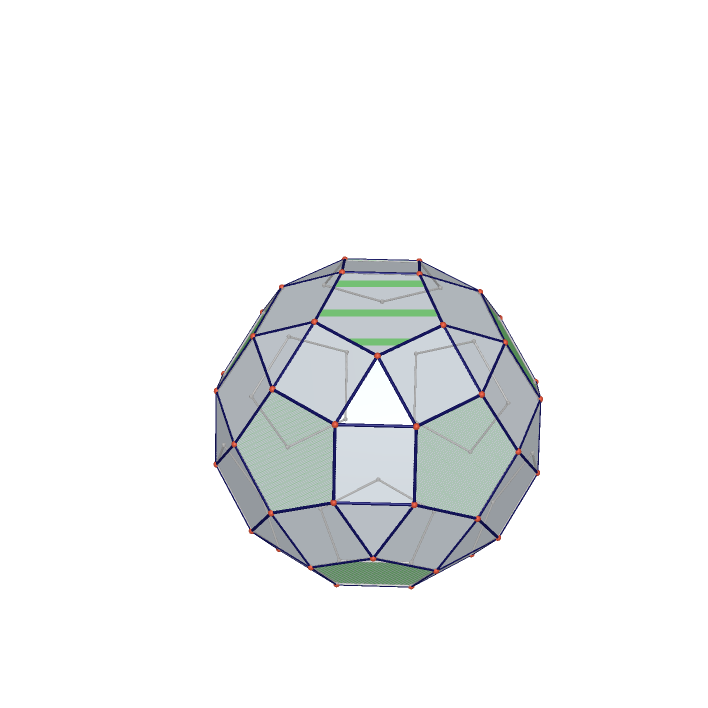
Parabola	Regular Octahedron Inside Cube	Rhombic Dodecahedrons in Icosahedron	Rhombicosidodecahedron

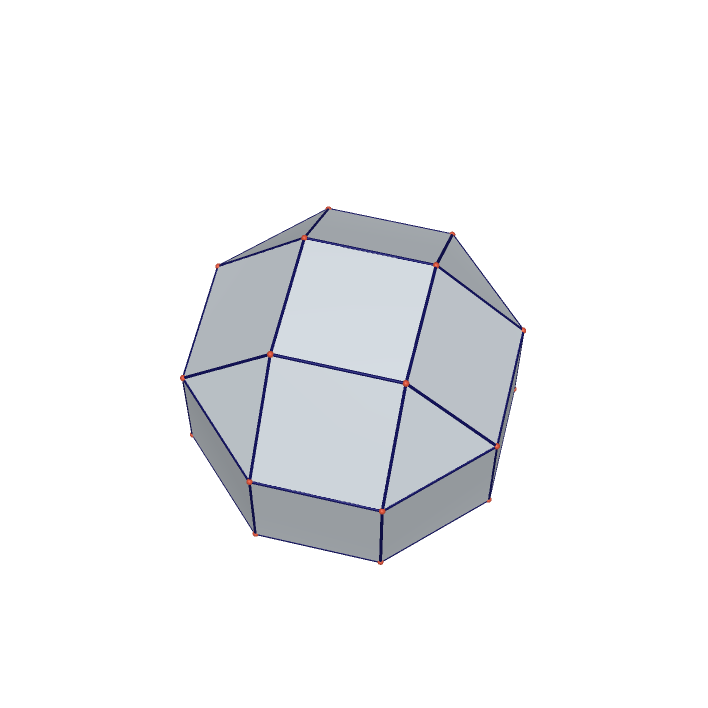
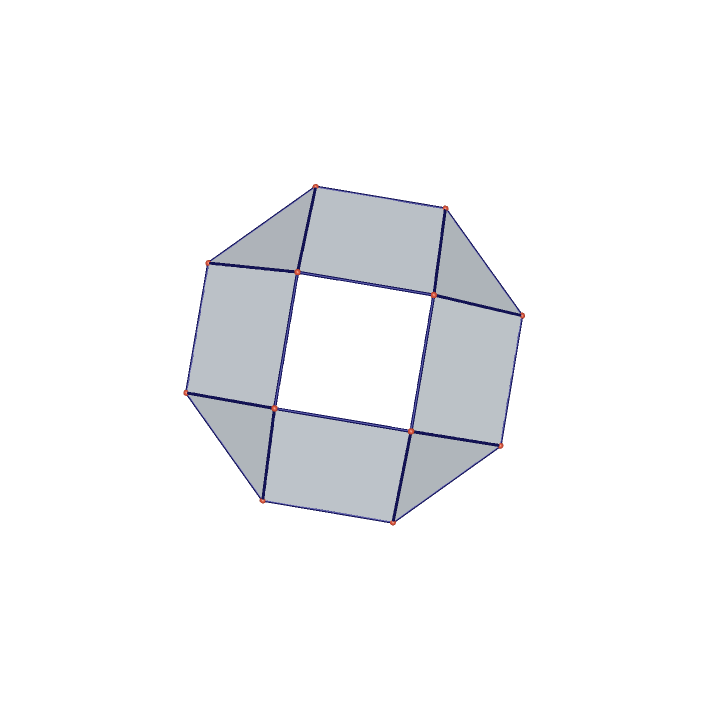
Rhombicuboctahedron	Square Cupola

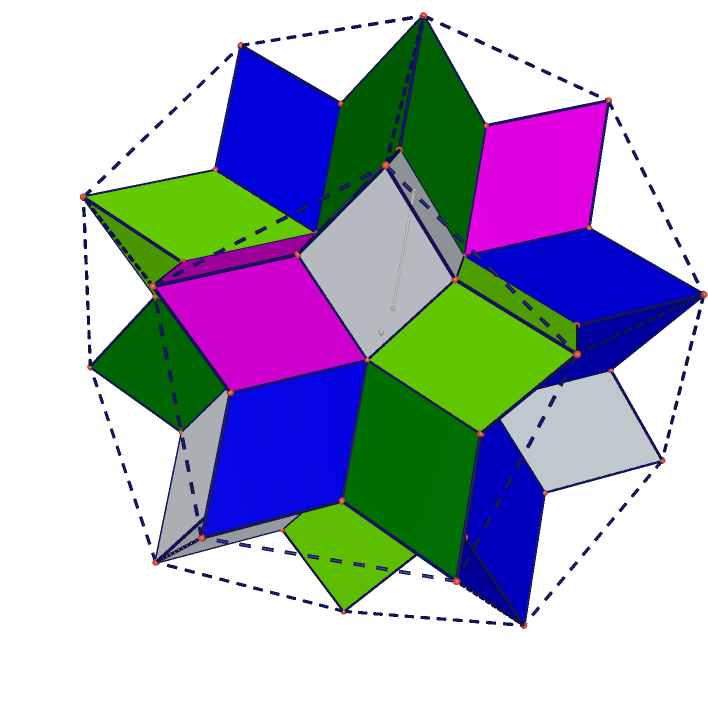
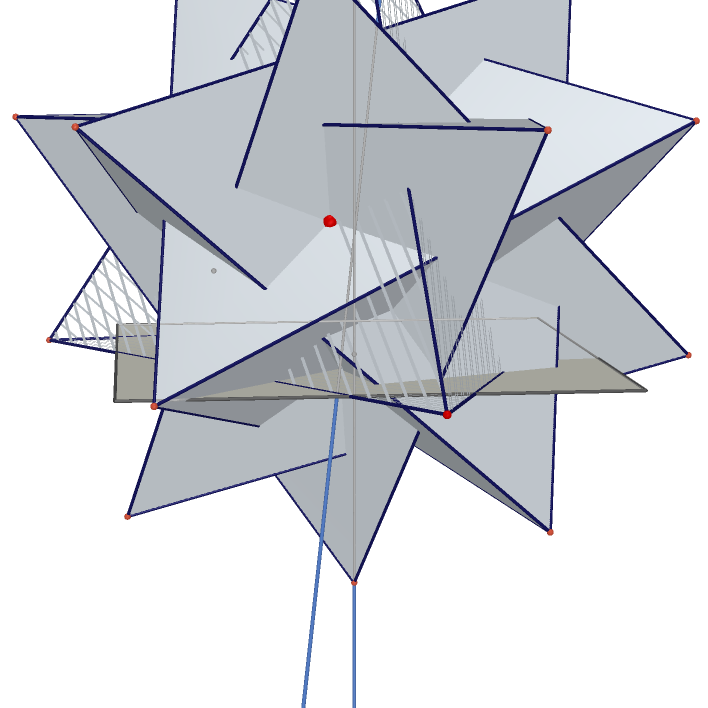
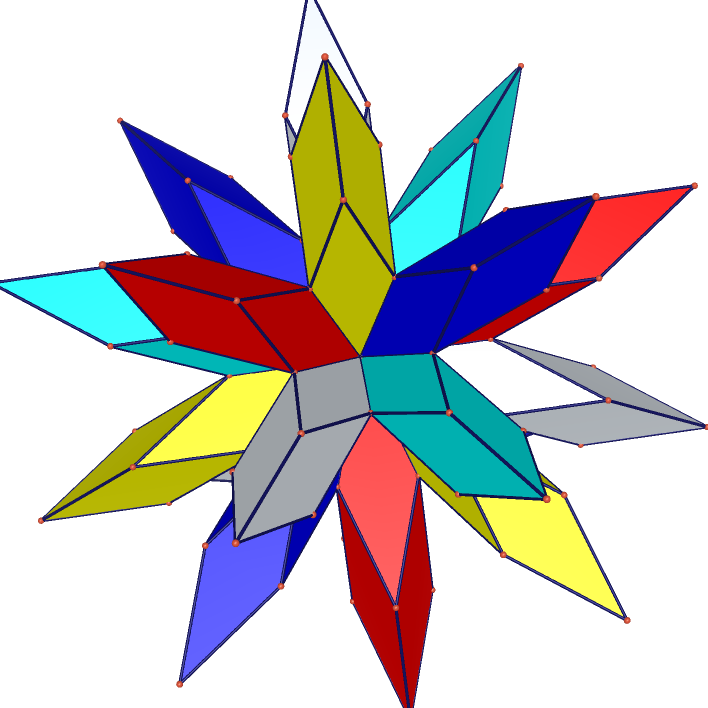
Steiner Porism with 6 Circles	Steiner Porism with 8 Circles	Stellation of Rhombic Dodecahedron

Tetrahedron Projected on Cube	The Large Regular Dodecahedron Contain A Cube	The Projection of a Cube on a Cube	The Projection of a Cube on Rhombic Triacontahedron	The Projection of a Terahedron on Terahedron	The Projection of a Tetrahedron on Cube	Three-circle Theorem on Sphere	Torus	Triangular Cupola

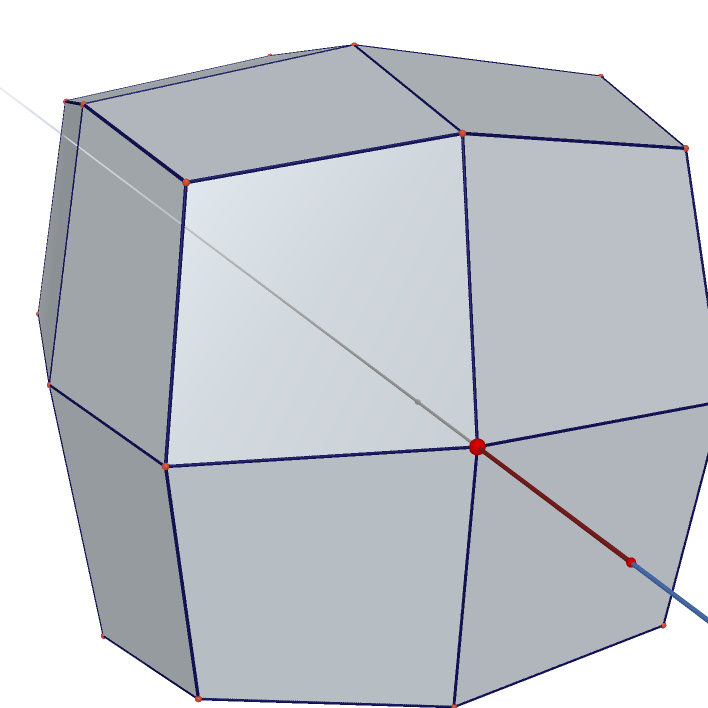
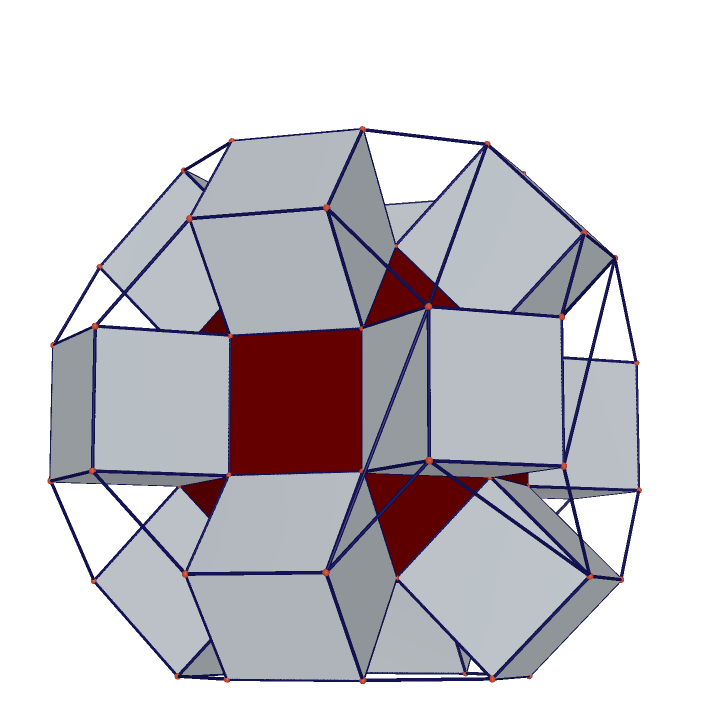
Truncated Cuboctahedron	Truncated icosidodecahedron	Villarceau Circles	Villarceau Circles with Animation